初中数学解直角三角形的应用-仰角俯角问题选择题

如图，垂直于水平面的 $5G$ 信号塔 AB建在垂直于水平面的悬崖边 B点处，某测量员从山脚 C点出发沿水平方向前行78米到 D点（点 A， B， C在同一直线上），再沿斜坡 $\mathit{DE}$ 方向前行78米到 E点（点 A， B， C， D， E在同一平面内），在点 E处测得 $5G$ 信号塔顶端 A的仰角为43°，悬崖 BC的高为144.5米，斜坡 DE的坡度（或坡比） $i＝1：2.4$ ，则信号塔 AB的高度约为（　　）

（参考数据： $\mathit{sin}43°\approx 0.68$ ， $\mathit{cos}43°\approx 0.73$ ， $\mathit{tan}43°\approx 0.93$ ）

A．

23米

B．

24米

C．

24.5米

D．

25米

如图，数学活动小组利用测角仪和皮尺测量学校旗杆的高度，在点D处测得旗杆顶端A的仰角 $\angle \mathit{ADE}为55°$，测角仪CD的高度为1米，其底端C与旗杆底端B之间的距离为6米，设旗杆AB的高度为x米，则下列关系式正确的是（　　）

A． $\mathit{tan}55°=\frac{6}{x-1}$B． $\mathit{tan}55°=\frac{x-1}{6}$

C． $\sin 55°=\frac{x-1}{6}$D． $\cos 55°=\frac{x-1}{6}$

如图，在离铁塔150米的 $A$处，用测倾仪测得塔顶的仰角为 $\alpha$，测倾仪高 $\mathit{AD}$为1.5米，则铁塔的高 $\mathit{BC}$为 $($　　 $)$

A． $(1.5+150\tan \alpha )$米B． $(1.5+\frac{150}{\tan \alpha })$米

C． $(1.5+150\sin \alpha )$米D． $(1.5+\frac{150}{\sin \alpha })$米

无人机在 $A$处测得正前方河流两岸 $B$、 $C$的俯角分别为 $\alpha =70°$、 $\beta =40°$，此时无人机的高度是 $h$，则河流的宽度 $\mathit{BC}$为 $($　　 $)$

A． $h(\tan 50°-\tan 20°)$B． $h(\tan 50°+\tan 20°)$

C． $h(\frac{1}{\tan 70°}-\frac{1}{\tan 40°})$D． $h(\frac{1}{\tan 70°}+\frac{1}{\tan 40°})$

如图，小亮为了测量校园里教学楼 $\mathit{AB}$的高度，将测角仪 $\mathit{CD}$竖直放置在与教学楼水平距离为 $18\sqrt{3}m$的地面上，若测角仪的高度是 $1.5m$．测得教学楼的顶部 $A$处的仰角为 $30°$．则教学楼的高度是 $($　　 $)$

A． $55.5m$B． $54m$C． $19.5m$D． $18m$

如图，数学实践活动小组要测量学校附近楼房 $\mathit{CD}$的高度，在水平地面 $A$处安置测倾器测得楼房 $\mathit{CD}$顶部点 $D$的仰角为 $45°$，向前走20米到达 $A\text{'}$处，测得点 $D$的仰角为 $67.5°$，已知测倾器 $\mathit{AB}$的高度为1.6米，则楼房 $\mathit{CD}$的高度约为（结果精确到0.1米， $\sqrt{2}\approx 1.414\left)\right($　　 $)$

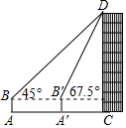
A．34.14米B．34.1米C．35.7米D．35.74米

聊城“水城之眼”摩天轮是亚洲三大摩天轮之一，也是全球首座建筑与摩天轮相结合的城市地标，如图，点 $O$是摩天轮的圆心，长为110米的 $\mathit{AB}$是其垂直地面的直径，小莹在地面 $C$点处利用测角仪测得摩天轮的最高点 $A$的仰角为 $33°$，测得圆心 $O$的仰角为 $21°$，则小莹所在 $C$点到直径 $\mathit{AB}$所在直线的距离约为 $(\tan 33°\approx 0.65$， $\tan 21°\approx 0.38\left)\right($　　 $)$

A．169米B．204米C．240米D．407米

济南大明湖畔的“超然楼”被称作“江北第一楼”，某校数学社团的同学对超然楼的高度进行了测量，如图，他们在 $A$处仰望塔顶，测得仰角为 $30°$，再往楼的方向前进 $60m$至 $B$处，测得仰角为 $60°$，若学生的身高忽略不计， $\sqrt{3}\approx 1.7$，结果精确到 $1m$，则该楼的高度 $\mathit{CD}$为 $($　　 $)$

A． $47m$B． $51m$C． $53m$D． $54m$

如图，为了测量某建筑物 $\mathit{MN}$的高度，在平地上 $A$处测得建筑物顶端 $M$的仰角为 $30°$，向 $N$点方向前进 $16m$到达 $B$处，在 $B$处测得建筑物顶端 $M$的仰角为 $45°$，则建筑物 $\mathit{MN}$的高度等于 $($　　 $)$

A． $8(\sqrt{3}+1)m$B． $8(\sqrt{3}-1)m$C． $16(\sqrt{3}+1)m$D． $16(\sqrt{3}-1)m$

小菁同学在数学实践活动课中测量路灯的高度．如图，已知她的目高 $\mathit{AB}$为1.5米，她先站在 $A$处看路灯顶端 $O$的仰角为 $35°$，再往前走3米站在 $C$处，看路灯顶端 $O$的仰角为 $65°$，则路灯顶端 $O$到地面的距离约为（已知 $\sin 35°\approx 0.6$， $\cos 35°\approx 0.8$， $\tan 35°\approx 0.7$， $\sin 65°\approx 0.9$， $\cos 65°\approx 0.4$， $\tan 65°\approx 2.1\left)\right($　　 $)$

A．3.2米B．3.9米C．4.7米D．5.4米

如图，热气球的探测器显示，从热气球A处看一栋楼顶部B处的仰角为30°，看这栋楼底部C处的俯角为60°，热气球A处与楼的水平距离为120m，则这栋楼的高度为（　　）

A． $160\sqrt{3}m$B． $120\sqrt{3}m$C． $300m$D． $160\sqrt{2}m$

如图，某日，正在我国南海海域作业的一艘大型渔船突然发生险情，相关部门接到求救信号后，立即调遣一架直升飞机和一艘正在南海巡航的渔政船前往救援，当飞机到达海面3000 m的高空 C处时，测得 A处渔政船的俯角为45°，测得 B处发生险情渔船的俯角为30°，此时渔政船和渔船的距离 AB是（　　）

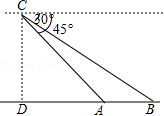
A．

$3000\sqrt{3}m$

B．

$3000(\sqrt{3}+1)m$

C．

$3000(\sqrt{3}-1)m$

D．

$1500\sqrt{3}m$

如图，学校环保社成员想测量斜坡 旁一棵树 的高度，他们先在点 处测得树顶 的仰角为 ，然后在坡顶 测得树顶 的仰角为 ，已知斜坡 的长度为 ， 的长为 ，则树 的高度是 　　 ．

A．

$20\sqrt{3}$

B．

30

C．

$30\sqrt{3}$

D．

40

如图，小明想要测量学校操场上旗杆 $\mathit{AB}$ 的高度，他作了如下操作：（1）在点 $C$ 处放置测角仪，测得旗杆顶的仰角 $\angle \mathit{ACE}=\alpha$ ；

（2）量得测角仪的高度 $\mathit{CD}=a$ ；

（3）量得测角仪到旗杆的水平距离 $\mathit{DB}=b$ ．

利用锐角三角函数解直角三角形的知识，旗杆的高度可表示为 $($ 　　 $)$

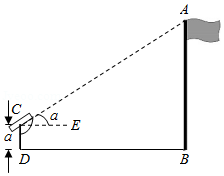
A．

$a+b\tan \alpha$

B．

$a+b\sin \alpha$

C．

$a+\frac{b}{\tan \alpha }$

D．

$a+\frac{b}{\sin \alpha }$

从一艘船上测得海岸上高为42米的灯塔顶部的仰角为 $30°$ 时，船离灯塔的水平距离是 $($ 　　 $)$

A．

$42\sqrt{3}$ 米

B．

$14\sqrt{3}$ 米

C．

21米

D．

42米