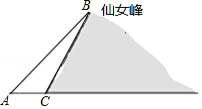
数学“综合与实践”课中,老师带领同学们来到娄底市郊区,测算如图所示的仙女峰的高度,李红盛同学利用已学的数学知识设计了一个实践方案,并实施了如下操作:先在水平地面 处测得山顶 的仰角 为 ,再由 沿水平方向前进377米到达山脚 处,测得山坡 的坡度为 ,请你求出仙女峰的高度(参考数据:
相关知识点
推荐套卷
数学“综合与实践”课中,老师带领同学们来到娄底市郊区,测算如图所示的仙女峰的高度,李红盛同学利用已学的数学知识设计了一个实践方案,并实施了如下操作:先在水平地面 处测得山顶 的仰角 为 ,再由 沿水平方向前进377米到达山脚 处,测得山坡 的坡度为 ,请你求出仙女峰的高度(参考数据:
