初中数学解直角三角形的应用-仰角俯角问题试题

如图，热气球的探测器显示，从热气球A处看一栋楼顶部B处的仰角为30°，看这栋楼底部C处的俯角为60°，热气球A处与楼的水平距离为120m，则这栋楼的高度为（　　）

A． $160\sqrt{3}m$B． $120\sqrt{3}m$C． $300m$D． $160\sqrt{2}m$

如图，某建筑物AC顶部有一旗杆AB，且点A，B，C在同一条直线上，小明在地面D处观测旗杆顶端B的仰角为30°，然后他正对建筑物的方向前进了20米到达地面的E处，又测得旗杆顶端B的仰角为60°，已知建筑物的高度 $\mathit{AC}＝12m$，求旗杆AB的高度（结果精确到0.1米）．参考数据： $\sqrt{3}\approx 1.73,\mathrm{}\sqrt{2}\approx 1.41$．

小宇在学习解直角三角形的知识后，萌生了测量他家对面位于同一水平面的楼房高度的想法，他站在自家C处测得对面楼房底端B的俯角为45°，测得对面楼房顶端A的仰角为30°，并量得两栋楼房间的距离为9米，请你用小宇测得的数据求出对面楼房AB的高度．（结果保留到整数，参考数据： $\sqrt{2}\approx 1.4,$ $\sqrt{3}\approx 1.7$）

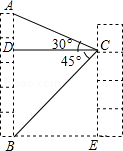
如图，某校教学楼 AC与实验楼 BD的水平间距 CD＝15 $\sqrt{3}$ 米，在实验楼顶部 B点测得教学楼顶部 A点的仰角是30°，底部 C点的俯角是45°，则教学楼 AC的高度是 　米（结果保留根号）．

如图所示，某施工队要测量隧道长度 BC， AD＝600米， AD⊥ BC，施工队站在点 D处看向 B，测得仰角为45°，再由 D走到 E处测量， DE∥ AC， ED＝500米，从点 E看向点 C，测得仰角为53°，求隧道 BC长．（sin53°≈ $\frac{4}{5}$ ，cos53°≈ $\frac{3}{5}$ ，tan53°≈ $\frac{4}{3}$ ）．

我市304国道通辽至霍林郭勒段在修建过程中经过一座山峰，如图所示，其中山脚 A、 C两地海拔高度约为1000米，山顶 B处的海拔高度约为1400米，由 B处望山脚 A处的俯角为30°，由 B处望山脚 C处的俯角为45°，若在 A、 C两地间打通一隧道，求隧道最短为多少米（结果取整数，参考数据 $\sqrt{3}$ ≈1.732）

如图，一座山的一段斜坡 BD的长度为600米，且这段斜坡的坡度 i＝1：3（沿斜坡从 B到 D时，其升高的高度与水平前进的距离之比）．已知在地面 B处测得山顶 A的仰角为33°，在斜坡 D处测得山顶 A的仰角为45°．求山顶 A到地面 BC的高度 AC是多少米？（结果用含非特殊角的三角函数和根式表示即可）

某班数学兴趣小组利用数学活动课时间测量位于烈山山顶的炎帝雕像高度，已知烈山坡面与水平面的夹角为30°，山高857.5尺，组员从山脚D处沿山坡向着雕像方向前进1620尺到达E点，在点E处测得雕像顶端A的仰角为60°，求雕像AB的高度．

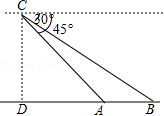
全球最大的关公塑像矗立在荆州古城东门外．如图，张三同学在东门城墙上C处测得塑像底部B处的俯角为11°48′，测得塑像顶部A处的仰角为45°，点D在观测点C正下方城墙底的地面上，若CD＝10米，则此塑像的高AB约为　　米（参考数据：tan78°12′≈4.8）．

如图，在办公楼AB和实验楼CD之间有一旗杆EF，从办公楼AB顶部A点处经过旗杆顶部E点恰好看到实验楼CD的底部D点，且俯角为45°，从实验楼CD顶部C点处经过旗杆顶部E点恰好看到办公楼AB的G点，BG＝1米，且俯角为30°，已知旗杆EF＝9米，求办公楼AB的高度．（结果精确到1米，参考数据： $\sqrt{2}\approx 1.41$， $\sqrt{3}\approx 1.73$）

在一次综合实践活动中，小明要测某地一座古塔 AE的高度．如图，已知塔基顶端 B（和 A、 E共线）与地面 C处固定的绳索的长 BC为80 m．她先测得∠ BCA＝35°，然后从 C点沿 AC方向走30 m到达 D点，又测得塔顶 E的仰角为50°，求塔高 AE．（人的高度忽略不计，结果用含非特殊角的三角函数表示）

如图，物理教师为同学们演示单摆运动，单摆左右摆动中，在 OA的位置时俯角∠ EOA＝30°，在 OB的位置时俯角∠ FOB＝60°，若 OC⊥ EF，点 A比点 B高7 cm．求：

（1）单摆的长度（ $\sqrt{3}$ ≈1.7）；

（2）从点 A摆动到点 B经过的路径长（π≈3.1）．

如图，某日，正在我国南海海域作业的一艘大型渔船突然发生险情，相关部门接到求救信号后，立即调遣一架直升飞机和一艘正在南海巡航的渔政船前往救援，当飞机到达海面3000 m的高空 C处时，测得 A处渔政船的俯角为45°，测得 B处发生险情渔船的俯角为30°，此时渔政船和渔船的距离 AB是（　　）

A．

$3000\sqrt{3}m$

B．

$3000(\sqrt{3}+1)m$

C．

$3000(\sqrt{3}-1)m$

D．

$1500\sqrt{3}m$

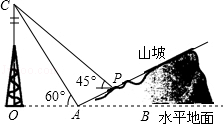
如图所示，某人在山坡坡脚A处测得电视塔尖点C的仰角为60°，沿山坡向上走到P处再测得C的仰角为45°，已知OA＝200米，山坡坡度为 $\frac{1}{3}$（即 $\tan \angle \mathit{PAB}=\frac{1}{3}$），且O，A，B在同一条直线上，求电视塔OC的高度以及此人所在的位置点P的垂直高度．（侧倾器的高度忽略不计，结果保留根号）

如图，学校环保社成员想测量斜坡 旁一棵树 的高度，他们先在点 处测得树顶 的仰角为 ，然后在坡顶 测得树顶 的仰角为 ，已知斜坡 的长度为 ， 的长为 ，则树 的高度是 　　 ．

A．

$20\sqrt{3}$

B．

30

C．

$30\sqrt{3}$

D．

40