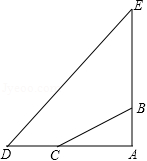
在一次综合实践活动中，小明要测某地一座古塔 AE的高度．如图，已知塔基顶端 B（和 A、 E共线）与地面 C处固定的绳索的长 BC为80 m．她先测得∠ BCA＝35°，然后从 C点沿 AC方向走30 m到达 D点，又测得塔顶 E的仰角为50°，求塔高 AE．（人的高度忽略不计，结果用含非特殊角的三角函数表示）
相关试题
下结论：
是等腰三角形，并说明理由。
∠1=∠3，∠C=110°，求∠2的度数。
相关知识点
推荐套卷
在一次综合实践活动中，小明要测某地一座古塔 AE的高度．如图，已知塔基顶端 B（和 A、 E共线）与地面 C处固定的绳索的长 BC为80 m．她先测得∠ BCA＝35°，然后从 C点沿 AC方向走30 m到达 D点，又测得塔顶 E的仰角为50°，求塔高 AE．（人的高度忽略不计，结果用含非特殊角的三角函数表示）
粤公网安备 44130202000953号