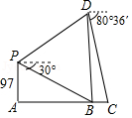
乌江快铁大桥是快铁渝黔线的一项重要工程,由主桥 和引桥 两部分组成(如图所示),建造前工程师用以下方式做了测量:无人机在 处正上方 处的 点,测得 处的俯角为 (当时 处被小山体阻挡无法观测).无人机飞行到 处正上方的 处时能看到 处,此时测得 处俯角为 .
(1)求主桥 的长度;
(2)若两观察点 、 的连线与水平方向的夹角为 ,求引桥 的长.
(长度均精确到 ,参考数据: , , ,
相关知识点
推荐套卷
乌江快铁大桥是快铁渝黔线的一项重要工程,由主桥 和引桥 两部分组成(如图所示),建造前工程师用以下方式做了测量:无人机在 处正上方 处的 点,测得 处的俯角为 (当时 处被小山体阻挡无法观测).无人机飞行到 处正上方的 处时能看到 处,此时测得 处俯角为 .
(1)求主桥 的长度;
(2)若两观察点 、 的连线与水平方向的夹角为 ,求引桥 的长.
(长度均精确到 ,参考数据: , , ,
