初中数学解直角三角形的应用-仰角俯角问题试题

如图所示，为了测量出一垂直水平地面的某高大建筑物 $\mathit{AB}$的高度，一测量人员在该建筑物附近 $C$处，测得建筑物顶端 $A$处的仰角大小为 $45°$，随后沿直线 $\mathit{BC}$向前走了100米后到达 $D$处，在 $D$处测得 $A$处的仰角大小为 $30°$，则建筑物 $\mathit{AB}$的高度约为　 　米．

（注：不计测量人员的身高，结果按四舍五入保留整数，参考数据： $\sqrt{2}\approx 1.41$， $\sqrt{3}\approx 1.73)$

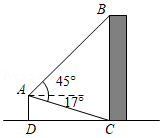
在黄冈长江大桥的东端一处空地上，有一块矩形的标语牌 $\mathit{ABCD}$（如图所示），已知标语牌的高 $\mathit{AB}=5m$，在地面的点 $E$处，测得标语牌点 $A$的仰角为 $30°$，在地面的点 $F$处，测得标语牌点 $A$的仰角为 $75°$，且点 $E$， $F$， $B$， $C$在同一直线上，求点 $E$与点 $F$之间的距离．（计算结果精确到0.1米，参考数据： $\sqrt{2}\approx 1.41$， $\sqrt{3}\approx 1.73)$

小明想要测量学校食堂和食堂正前方一棵树的高度，他从食堂楼底 $M$处出发，向前走3米到达 $A$处，测得树顶端 $E$的仰角为 $30°$，他又继续走下台阶到达 $C$处，测得树的顶端 $E$的仰角是 $60°$，再继续向前走到大树底 $D$处，测得食堂楼顶 $N$的仰角为 $45°$．已知点离地面的高度 $\mathit{AB}=2$米， $\angle \mathit{BCA}=30°$，且 $B$、 $C$、 $D$三点在同一直线上．

（1）求树 $\mathit{DE}$的高度；

（2）求食堂 $\mathit{MN}$的高度．

某数学兴趣小组去测量一座小山的高度，在小山顶上有一高度为20米的发射塔 $\mathit{AB}$，如图所示．在山脚平地上的 $D$处测得塔底 $B$的仰角为 $30°$，向小山前进80米到达点 $E$处，测得塔顶 $A$的仰角为 $60°$，求小山 $\mathit{BC}$的高度．

如图是某商场营业大厅自动扶梯示意图．自动扶梯 $\mathit{AB}$的倾斜角为 $30°$，在自动扶梯下方地面 $C$处测得扶梯顶端 $B$的仰角为 $60°$， $A$、 $C$之间的距离为 $4m$．则自动扶梯的垂直高度 $\mathit{BD}=$　　 $m$．（结果保留根号）

如图，无人机于空中 $A$处测得某建筑顶部 $B$处的仰角为 $45°$，测得该建筑底部 $C$处的俯角为 $17°$．若无人机的飞行高度 $\mathit{AD}$为 $62m$，则该建筑的高度 $\mathit{BC}$为　    　 $m$．

（参考数据： $\sin 17°\approx 0.29$， $\cos 17°\approx 0.96$， $\tan 17°\approx 0.31)$

热气球的探测器显示，从热气球 $A$处看大楼 $\mathit{BC}$顶部 $C$的仰角为 $30°$，看大楼底部 $B$的俯角为 $45°$，热气球与该楼的水平距离 $\mathit{AD}$为60米，求大楼 $\mathit{BC}$的高度．（结果精确到1米，参考数据： $\sqrt{3}\approx 1.73)$

如图，小亮为了测量校园里教学楼 $\mathit{AB}$的高度，将测角仪 $\mathit{CD}$竖直放置在与教学楼水平距离为 $18\sqrt{3}m$的地面上，若测角仪的高度是 $1.5m$．测得教学楼的顶部 $A$处的仰角为 $30°$．则教学楼的高度是 $($　　 $)$

A． $55.5m$B． $54m$C． $19.5m$D． $18m$

如图，山顶有一塔 $\mathit{AB}$，塔高 $33m$．计划在塔的正下方沿直线 $\mathit{CD}$开通穿山隧道 $\mathit{EF}$．从与 $E$点相距 $80m$的 $C$处测得 $A$、 $B$的仰角分别为 $27°$、 $22°$，从与 $F$点相距 $50m$的 $D$处测得 $A$的仰角为 $45°$．求隧道 $\mathit{EF}$的长度．

（参考数据： $\tan 22°\approx 0.40$， $\tan 27°\approx 0.51$． $)$

如图，小强想测量楼 $\mathit{CD}$的高度，楼在围墙内，小强只能在围墙外测量，他无法测得观测点到楼底的距离，于是小强在 $A$处仰望楼顶，测得仰角为 $37°$，再往楼的方向前进30米至 $B$处，测得楼顶的仰角为 $53°(A$， $B$， $C$三点在一条直线上），求楼 $\mathit{CD}$的高度（结果精确到0.1米，小强的身高忽略不计）．

如图，在数学活动课上，小丽为了测量校园内旗杆 $\mathit{AB}$的高度，站在教学楼的 $C$处测得旗杆底端 $B$的俯角为 $45°$，测得旗杆顶端 $A$的仰角为 $30°$．已知旗杆与教学楼的距离 $\mathit{BD}=9m$，请你帮她求出旗杆的高度（结果保留根号）．

如图，甲、乙为两座建筑物，它们之间的水平距离 $\mathit{BC}$为 $30m$，在 $A$点测得 $D$点的仰角 $\angle \mathit{EAD}$为 $45°$，在 $B$点测得 $D$点的仰角 $\angle \mathit{CBD}$为 $60°$，求这两座建筑物的高度（结果保留根号）

如图，建筑物 $\mathit{AB}$的高为 $6m$，在其正东方向有一个通信塔 $\mathit{CD}$，在它们之间的地面点 $M(B$， $M$， $D$三点在一条直线上）处测得建筑物顶端 $A$，塔顶 $C$的仰角分别为 $37°$和 $60°$，在 $A$处测得塔顶 $C$的仰角为 $30°$，则通信塔 $\mathit{CD}$的高度． $(\tan 37°\approx 0.75,0.01m)$

如图，某校数学兴趣小组为测得校园里旗杆 $\mathit{AB}$的高度，在操场的平地上选择一点 $C$，测得旗杆顶端 $A$的仰角为 $30°$，再向旗杆的方向前进16米，到达点 $D$处 $(C$、 $D$、 $B$三点在同一直线上），又测得旗杆顶端 $A$的仰角为 $45°$，请计算旗杆 $\mathit{AB}$的高度（结果保留根号）．

成都“339”电视塔作为成都市地标性建筑之一，现已成为外地游客到成都旅游打卡的网红地．如图，为测量电视塔观景台 $A$处的高度，某数学兴趣小组在电视塔附近一建筑物楼项 $D$处测得塔 $A$处的仰角为 $45°$，塔底部 $B$处的俯角为 $22°$．已知建筑物的高 $\mathit{CD}$约为61米，请计算观景台的高 $\mathit{AB}$的值．

（结果精确到1米；参考数据： $\sin 22°\approx 0.37$， $\cos 22°\approx 0.93$， $\tan 22°\approx 0.40)$