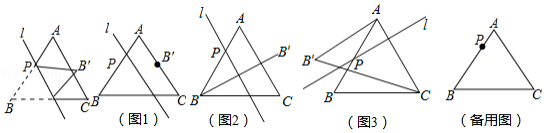
如图,已知等边 的边长为8,点 是 边上的一个动点(与点 、 不重合).直线 是经过点 的一条直线,把 沿直线 折叠,点 的对应点是点 .
(1)如图1,当 时,若点 恰好在 边上,则 的长度为 ;
(2)如图2,当 时,若直线 ,则 的长度为 ;
(3)如图3,点 在 边上运动过程中,若直线 始终垂直于 , 的面积是否变化?若变化,说明理由;若不变化,求出面积;
(4)当 时,在直线 变化过程中,求 面积的最大值.
已知等边三角形 ,过 点作 的垂线 ,点 为 上一动点(不与点 重合),连接 ,把线段 绕点 逆时针方向旋转 得到 ,连 .
(1)如图1,直接写出线段 与 的数量关系;
(2)如图2,当点 、 在 同侧且 时,求证:直线 垂直平分线段 ;
(3)如图3,若等边三角形 的边长为4,点 、 分别位于直线 异侧,且 的面积等于 ,求线段 的长度.

如图1,点 坐标为 ,以 为边在第一象限内作等边 ,点 为 轴上一动点,且在点 右侧,连接 ,以 为边在第一象限内作等边 ,连接 交 于 .

(1)①直接回答: 与 全等吗?
②试说明:无论点 如何移动, 始终与 平行;
(2)当点 运动到使 时,如图2,经过 、 、 三点的抛物线为 .试问: 上是否存在动点 ,使 为直角三角形且 为直角边?若存在,求出点 坐标;若不存在,说明理由;
(3)在(2)的条件下,将 沿 轴翻折得 ,设 与 组成的图形为 ,函数 的图象 与 有公共点.试写出: 与 的公共点为3个时, 的取值.
如图,在矩形 中,点 为坐标原点,点 的坐标为 ,点 、 在坐标轴上,点 在 边上,直线 ,直线 .
(1)分别求直线 与 轴,直线 与 的交点坐标;
(2)已知点 在第一象限,且是直线 上的点,若 是等腰直角三角形,求点 的坐标;
(3)我们把直线 和直线 上的点所组成的图形为图形 .已知矩形 的顶点 在图形 上, 是坐标平面内的点,且 点的横坐标为 ,请直接写出 的取值范围(不用说明理由).

数学活动课上,某学习小组对有一内角为 的平行四边形 进行探究:将一块含 的直角三角板如图放置在平行四边形 所在平面内旋转,且 角的顶点始终与点 重合,较短的直角边和斜边所在的两直线分别交线段 , 于点 , (不包括线段的端点).
(1)初步尝试
如图1,若 ,求证:① ,② ;
(2)类比发现
如图2,若 ,过点 作 于点 ,求证: ;
(3)深入探究
如图3,若 ,探究得: 的值为常数 ,则 .

【问题情景】
利用三角形的面积相等来求解的方法是一种常见的等积法,此方法是我们解决几何问题的途径之一.
例如:张老师给小聪提出这样一个问题:
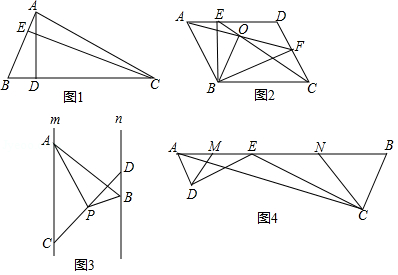
如图1,在△ ABC中, AB=3, BC=6,问△ ABC的高 AD与 CE的比是多少?
小聪的计算思路是:
根据题意得: S △ ABC= BC• AD= AB• CE.
从而得2 AD= CE,∴ =
请运用上述材料中所积累的经验和方法解决下列问题:
(1)【类比探究】
如图2,在▱ ABCD中,点 E、 F分别在 AD, CD上,且 AF= CE,并相交于点 O,连接 BE、 BF,
求证: BO平分角 AOC.
(2)【探究延伸】
如图3,已知直线 m∥ n,点 A、 C是直线 m上两点,点 B、 D是直线 n上两点,点 P是线段 CD中点,且∠ APB=90°,两平行线 m、 n间的距离为4.求证: PA• PB=2 AB.
(3)【迁移应用】
如图4, E为 AB边上一点, ED⊥ AD, CE⊥ CB,垂足分别为 D, C,∠ DAB=∠ B, AB= , BC=2, AC= ,又已知 M、 N分别为 AE、 BE的中点,连接 DM、 CN.求△ DEM与△ CEN的周长之和.
如图, 和
和 是有公共顶点的等腰直角三角形,
是有公共顶点的等腰直角三角形, ,点
,点 为射线
为射线 ,
, 的交点.
的交点.
(1)求证: ;
;
(2)若 ,
, ,把
,把 绕点
绕点 旋转,
旋转,
①当 时,求
时,求 的长;
的长;
②直接写出旋转过程中线段 长的最小值与最大值.
长的最小值与最大值.

如图,矩形 中,点 为 上一点, 为 的中点,且 .
(1)当 为 中点时,求证: ;
(2)当 时,求 的值;
(3)设 , ,作点 关于 的对称点 ,连接 , ,若点 到 的距离是 ,求 的值.
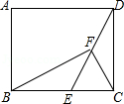
在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根.比如对于方程 ,操作步骤是:
第一步:根据方程的系数特征,确定一对固定点 , ;
第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点 ,另一条直角边恒过点 ;
第三步:在移动过程中,当三角板的直角顶点落在 轴上点 处时,点 的横坐标 即为该方程的一个实数根(如图 ;
第四步:调整三角板直角顶点的位置,当它落在 轴上另一点 处时,点 的横坐标 即为该方程的另一个实数根.

(1)在图2中,按照“第四步”的操作方法作出点 (请保留作出点 时直角三角板两条直角边的痕迹);
(2)结合图1,请证明“第三步”操作得到的 就是方程 的一个实数根;
(3)上述操作的关键是确定两个固定点的位置.若要以此方法找到一元二次方程 的实数根,请你直接写出一对固定点的坐标;
(4)实际上,(3)中的固定点有无数对,一般地,当 , , , 与 , , 之间满足怎样的关系时,点 , , , 就是符合要求的一对固定点?
如图,在正方形 中,点 在边 上(不与点 , 重合),连接 ,作 于点 , 于点 ,设 .
(1)求证: .
(2)连接 , ,设 , .求证: .
(3)设线段 与对角线 交于点 , 和四边形 的面积分别为 和 ,求 的最大值.

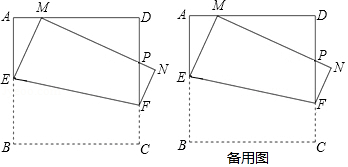
如图,在边长为1的正方形 中,动点 、 分别在边 、 上,将正方形 沿直线 折叠,使点 的对应点 始终落在边 上(点 不与点 、 重合),点 落在点 处, 与 交于点 ,设 .
(1)当 时,求 的值;
(2)随着点 在边 上位置的变化, 的周长是否发生变化?如变化,请说明理由;如不变,请求出该定值;
(3)设四边形 的面积为 ,求 与 之间的函数表达式,并求出 的最小值.
如图,在 中, AB AD.

(1)用尺规完成以下基本作图:在 AB上截取 AE,使得 AE= AD;作∠ BCD的平分线交 AB于点 F.(保留作图痕迹,不写作法)
(2)在(1)所作的图形中,连接 DE交 CF于点 P,猜想△ CDP按角分类的类型,并证明你的结论.
如图,在 中, ,点 是斜边 上一点,且 .
(1)作 的平分线,交 于点 ;(要求尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接 ,求证: .

如图,沿 方向开山修路.为了加快施工进度,要在小山的另一边同时施工,从 上的一点 取 , , .那么另一边开挖点 离 多远正好使 , , 三点在一直线上 取1.732,结果取整数)?
