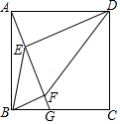
如图,在正方形 中,点 在边 上(不与点 , 重合),连接 ,作 于点 , 于点 ,设 .
(1)求证: .
(2)连接 , ,设 , .求证: .
(3)设线段 与对角线 交于点 , 和四边形 的面积分别为 和 ,求 的最大值.
推荐套卷
如图,在正方形 中,点 在边 上(不与点 , 重合),连接 ,作 于点 , 于点 ,设 .
(1)求证: .
(2)连接 , ,设 , .求证: .
(3)设线段 与对角线 交于点 , 和四边形 的面积分别为 和 ,求 的最大值.
