已知Rt△ABC中,AC=BC=2.一直角的顶点P在AB上滑动,直角的两边分别交线段AC,BC于E.F两点
(1)如图1,当 且PE⊥AC时,求证:
且PE⊥AC时,求证: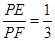 ;
;
(2)如图2,当 时(1)的结论是否仍然成立?为什么?
时(1)的结论是否仍然成立?为什么?
(3)在(2)的条件下,将直角∠EPF绕点P旋转,设∠BPF=α(0°<α<90°).连结EF,当△CEF的周长等于2+ 时,请直接写出α的度数.
时,请直接写出α的度数.
相关知识点
推荐套卷
已知Rt△ABC中,AC=BC=2.一直角的顶点P在AB上滑动,直角的两边分别交线段AC,BC于E.F两点
(1)如图1,当 且PE⊥AC时,求证:
且PE⊥AC时,求证: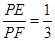 ;
;
(2)如图2,当 时(1)的结论是否仍然成立?为什么?
时(1)的结论是否仍然成立?为什么?
(3)在(2)的条件下,将直角∠EPF绕点P旋转,设∠BPF=α(0°<α<90°).连结EF,当△CEF的周长等于2+ 时,请直接写出α的度数.
时,请直接写出α的度数.