已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，点A，C的坐标分别为A（﹣3，0），C（1，0），tan∠BAC=
．
（1）写出点B的坐标；
（2）在x轴上找一点D，连接BD，使得△ADB与△ABC相似（不包括全等），并求点D的坐标；
（3）在（2）的条件下，如P，Q分别是AB和AD上的动点，连接PQ，设AP=DQ=m，问是否存在这样的m使得△APQ与△ADB相似？如存在，请求出的m值；如不存在，请说明理由．
相关试题
中，点
为
边上的一点，
．
．
的长及
在解题目：“先化简代数式
，再求值，其中，
”时，聪聪认为
只要任取一个使原式有意义的值代入都有相同的结果．你认为他说的有道理吗，如果他说的有道理，请求出这个结果，并说明理由．
，且
．
的值；
的值．
处6米处折断倒下，量得树梢
处与树底
处的长是8米，树干
与地面
垂直．试通过计算求出这棵大树原来的高度．
，其中
，且
为整数．相关知识点
推荐套卷
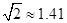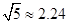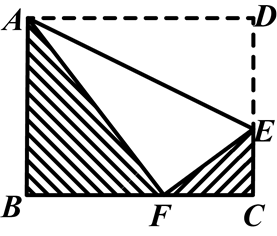
粤公网安备 44130202000953号