【问题情景】
利用三角形的面积相等来求解的方法是一种常见的等积法,此方法是我们解决几何问题的途径之一.
例如:张老师给小聪提出这样一个问题:
如图1,在△ ABC中, AB=3, BC=6,问△ ABC的高 AD与 CE的比是多少?
小聪的计算思路是:
根据题意得: S △ ABC= BC• AD= AB• CE.
从而得2 AD= CE,∴ =
请运用上述材料中所积累的经验和方法解决下列问题:
(1)【类比探究】
如图2,在▱ ABCD中,点 E、 F分别在 AD, CD上,且 AF= CE,并相交于点 O,连接 BE、 BF,
求证: BO平分角 AOC.
(2)【探究延伸】
如图3,已知直线 m∥ n,点 A、 C是直线 m上两点,点 B、 D是直线 n上两点,点 P是线段 CD中点,且∠ APB=90°,两平行线 m、 n间的距离为4.求证: PA• PB=2 AB.
(3)【迁移应用】
如图4, E为 AB边上一点, ED⊥ AD, CE⊥ CB,垂足分别为 D, C,∠ DAB=∠ B, AB= , BC=2, AC= ,又已知 M、 N分别为 AE、 BE的中点,连接 DM、 CN.求△ DEM与△ CEN的周长之和.

相关知识点
推荐套卷
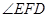 的度数.
的度数.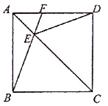

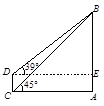
 ,再选一个你喜欢的数代入求值:
,再选一个你喜欢的数代入求值: 粤公网安备 44130202000953号
粤公网安备 44130202000953号