目前世界上最高的电视塔是广州新电视塔．如图8所示，新电视塔高AB为610米，远处有一栋大楼，某人在楼底C处测得塔顶B的仰角为45°，在楼顶D处测得塔顶B的仰角为39°，（sin39°≈0.63,cos39°≈0.78 , tan39°≈0.81）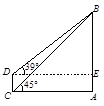
求大楼与电视塔之间的距离AC；
求大楼的高度CD（精确到1米）
相关试题
相关知识点
推荐套卷
目前世界上最高的电视塔是广州新电视塔．如图8所示，新电视塔高AB为610米，远处有一栋大楼，某人在楼底C处测得塔顶B的仰角为45°，在楼顶D处测得塔顶B的仰角为39°，（sin39°≈0.63,cos39°≈0.78 , tan39°≈0.81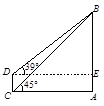）求大楼与电视塔之间的距离AC；
求大楼的高度CD（精确到1米）
粤公网安备 44130202000953号