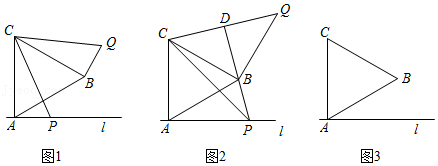
已知等边三角形 ,过 点作 的垂线 ,点 为 上一动点(不与点 重合),连接 ,把线段 绕点 逆时针方向旋转 得到 ,连 .
(1)如图1,直接写出线段 与 的数量关系;
(2)如图2,当点 、 在 同侧且 时,求证:直线 垂直平分线段 ;
(3)如图3,若等边三角形 的边长为4,点 、 分别位于直线 异侧,且 的面积等于 ,求线段 的长度.
相关知识点
推荐套卷
已知等边三角形 ,过 点作 的垂线 ,点 为 上一动点(不与点 重合),连接 ,把线段 绕点 逆时针方向旋转 得到 ,连 .
(1)如图1,直接写出线段 与 的数量关系;
(2)如图2,当点 、 在 同侧且 时,求证:直线 垂直平分线段 ;
(3)如图3,若等边三角形 的边长为4,点 、 分别位于直线 异侧,且 的面积等于 ,求线段 的长度.
