翔志琼公司修筑一条公路,开始修筑若干天以后,公司抽调了一部力量去完成其他任务,所以施工速度有所降低。修筑公路的里程y(千米)和所用时间x(天)的关系用下图所示的折线OAB表示,其中OA所在的直线是函数y=0.1x的图象,AB所在直线是函数y=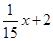 的图象。
的图象。
(1)求点A的坐标;
(2)完成修路工程后,公司发现如果一直按开始的速度修筑此公路,可提前20天完工,求此公路的长度。
相关知识点
推荐套卷
翔志琼公司修筑一条公路,开始修筑若干天以后,公司抽调了一部力量去完成其他任务,所以施工速度有所降低。修筑公路的里程y(千米)和所用时间x(天)的关系用下图所示的折线OAB表示,其中OA所在的直线是函数y=0.1x的图象,AB所在直线是函数y=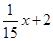 的图象。
的图象。
(1)求点A的坐标;
(2)完成修路工程后,公司发现如果一直按开始的速度修筑此公路,可提前20天完工,求此公路的长度。