数学活动课上，某学习小组对有一内角为 的平行四边形 进行探究：将一块含 的直角三角板如图放置在平行四边形 所在平面内旋转，且 角的顶点始终与点 重合，较短的直角边和斜边所在的两直线分别交线段 ， 于点 ， （不包括线段的端点）．
（1）初步尝试
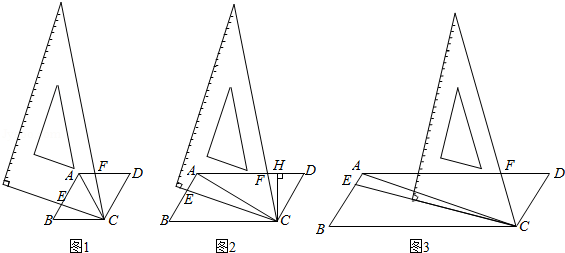
如图1，若 ，求证：① ，② ；
（2）类比发现
如图2，若 ，过点 作 于点 ，求证： ；
（3）深入探究
如图3，若 ，探究得： 的值为常数 ，则 ．
相关试题
学校准备五一组织老师去隆中参加诸葛亮文化节，现有甲、乙两家旅行社表示对老师优惠，设参加文化节的老师有x人，甲、乙两家旅行社实际收费为
、
，且它们的函数图象如图所示，根据图象信息，请你回答下列问题：
（1）当参加老师的人数为多少时，两家旅行社收费相同？
（2）当参加老师的人数为多少人时，选择甲旅行社合算？
（3）如果全共有50人参加时，选择哪家旅行社合算？
黄集中学八年级二班准备外出进行野外考察活动，需要租用一辆大客车一天，现有甲、乙两辆客车租用方案：甲车每天租金180元，另按实际行程每千米加收2元；乙车每天租金140元，另按实际行程每千米加收2.5元。若你是班长，同学们要到100千米以内的某地，为了节省费用，请你决定租用哪辆车合算？
在同一坐标系下，函数
的图象如图所示：请根据图象回答：
（1）方程组
的解为＿＿＿＿＿。
（2）不等式
的解集为＿＿＿＿＿。
（3）方程
的解为＿＿＿＿＿。
（4）不等式
的解集为＿＿＿＿＿。
的图象，并利用图象解答下列问题：
；（3）不等式
，请回答下列问题：
的值等于0?
的值恒小于0？推荐套卷
粤公网安备 44130202000953号