初中数学试题

综合与实践

【问题情境】

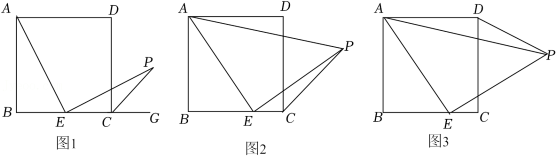
数学活动课上，老师出示了一个问题：如图1，在正方形 $ABCD$中，E是BC的中点， $AE\perp EP$， $EP$与正方形的外角 $\angle DCG$的平分线交于 $P$点．试猜想 $AE$与 $EP$的数量关系，并加以证明；

【思考尝试】

（1）同学们发现，取 $AB$的中点 $F$，连接 $EF$可以解决这个问题．请在图1中补全图形，解答老师提出的问题．

【实践探究】

（2）希望小组受此问题启发，逆向思考这个题目，并提出新的问题：如图2，在正方形 $ABCD$中， $E$为 $BC$边上一动点（点 $E，B$不重合）， $△AEP$是等腰直角三角形， $\angle AEP＝90°$，连接 $CP$，可以求出 $\angle DCP$的大小，请你思考并解答这个问题．

【拓展迁移】

（3）突击小组深入研究希望小组提出的这个问题，发现并提出新的探究点：如图3，在正方形 $ABCD$中， $E$为 $BC$边上一动点（点 $E，B$不重合）， $△AEP$是等腰直角三角形， $\angle AEP＝90°$，连接 $DP$．知道正方形的边长时，可以求出 $△ADP$周长的最小值．当 $AB＝4$时，请你求出 $△ADP$周长的最小值．

如图，已知抛物线 $y＝a{x}^2+bx+3（a\ne 0）$与 $x$轴交于 $A（1，0），B（4，0）$两点，与 $y$轴交于点 $C$，点 $D$为抛物线的顶点．

（1）求抛物线的函数表达式及点 $D$的坐标；

（2）若四边形 $BCEF$为矩形， $CE＝3$．点 $M$以每秒 $1$个单位的速度从点 $C$沿 $CE$向点 $E$运动，同时点 $N$以每秒 $2$个单位的速度从点 $E$沿 $EF$向点 $F$运动，一点到达终点，另一点随之停止．当以 $M、E、N$为顶点的三角形与 $△BOC$相似时，求运动时间 $t$的值；

（3）抛物线的对称轴与 $x$轴交于点 $P$，点 $G$是点 $P$关于点 $D$的对称点，点 $Q$是 $x$轴下方抛物线上的动点．若过点 $Q$的直线 $\mathrm{l}：\mathrm{y}＝\mathrm{kx}+\mathrm{m}（\left|\mathrm{k}\right|\mathrm{＜}\frac{9}{4}）$与抛物线只有一个公共点，且分别与线段 $GA、GB$相交于点 $H、K$，求证： $GH+GK$为定值．

综合与实践

综合与实践课上，老师让同学们以“矩形的折叠”为主题开展数学活动．

（1）操作判断

操作一：对折矩形纸片 $ABCD$，使 $AD$与 $BC$重合，得到折痕 $EF$，把纸片展平；

操作二：在 $AD$上选一点 $P$，沿 $BP$折叠，使点 $A$落在矩形内部点 $M$处，把纸片展平，连接 $PM，BM$．

根据以上操作，当点 $M$在 $EF$上时，写出图1中一个 $30°$的角：＿＿＿＿＿＿．

（2）迁移探究

小华将矩形纸片换成正方形纸片，继续探究，过程如下：

将正方形纸片 $ABCD$按照（1）中的方式操作，并延长 $PM$交 $CD$于点 $Q$，连接 $BQ$．

①如图2，当点 $M$在 $EF$上时， $\angle MBQ＝$＿＿＿＿＿＿ $°$， $\angle CBQ＝$＿＿＿＿＿＿ $°$；

②改变点 $P$在 $AD$上的位置（点 $P$不与点 $A，D$重合），如图3，判断 $\angle MBQ$与 $\angle CBQ$的数量关系，并说明理由．

（3）拓展应用

在（2）的探究中，已知正方形纸片 $ABCD$的边长为 $8cm$，当 $FQ＝1cm$时，直接写出 $AP$的长．

如图1，在矩形 $ABCD$中， $AB＝4，AD＝3$，点 $O$是边 $AB$上一个动点（不与点 $A$重合），连接 $EG$ $OD$，将 $△OAD$沿 $OD$折叠，得到 $△OED$；再以 $O$为圆心， $OA$的长为半径作半圆，交射线 $AB$于 $G$，连接 $AE$并延长交射线 $BC$于 $F$，连接，设 $OA＝x$．

（1）求证： $DE$是半圆 $O$的切线：

（2）当点 $E$落在 $BD$上时，求 $x$的值；

（3）当点 $E$落在 $BD$下方时，设 $△AGE$与 $△AFB$面积的比值为 $y$，确定 $y$与 $x$之间的函数关系式；

（4）直接写出：当半圆 $O$与 $△BCD$的边有两个交点时， $x$的取值范围．

抛物线 $y＝x^2﹣2x﹣3$交 $x$轴于 $A，B$两点（ $A$在 $B$的左边）， $C$是第一象限抛物线上一点，直线 $AC$交 $y$轴于点 $P$．

（1）直接写出 $A，B$两点的坐标；

（2）如图（1），当 $OP＝OA$时，在抛物线上存在点 $D$（异于点 $B$），使 $B，D$两点到 $AC$的距离相等，求出所有满足条件的点 $D$的横坐标；

（3）如图（2），直线 $BP$交抛物线于另一点 $E$，连接 $CE$交 $y$轴于点 $F$，点 $C$的横坐标为 $m$．求 $\frac{\mathit{FP}}{\mathit{OP}}$的值（用含 $m$的式子表示）．

如图，在平面直角坐标系中，抛物线 $y＝a{x}^2+bx﹣3$经过点 $B（6，0）$和点 $D（4，﹣3）$，与 $x$轴的另一个交点为 $A$，与 $y$轴交于点 $C$，作直线 $AD$．

（1）①求抛物线的函数表达式；

②直接写出直线 $AD$的函数表达式；

（2）点 $E$是直线 $AD$下方的抛物线上一点，连接 $BE$交 $AD$于点 $F$，连接 $BD，DE$， $△BDF$的面积记为 $S_1$， $△DEF$的面积记为 $S_2$，当 $S_1＝2S_2$时，求点 $E$的坐标；

（3）点 $G$为抛物线的顶点，将抛物线图象中 $x$轴下方的部分沿 $x$轴向上翻折，与抛物线剩下的部分组成新的曲线记为 $C_1$，点 $C$的对应点为 $C\prime$，点 $G$的对应点为 $G\prime$，将曲线 $C_1$沿 $y$轴向下平移 $n$个单位长度 $（0＜n＜6）$．曲线 $C_1$与直线 $BC$的公共点中，选两个公共点记作点 $P$和点 $Q$，若四边形 $C\prime G\prime QP$是平行四边形，直接写出点 $P$的坐标．

【特例感知】

（1）如图1， $△AOB$和 $△COD$是等腰直角三角形， $\angle AOB＝\angle COD＝90°$，点 $C$在 $OA$上，点 $D$在 $BO$的延长线上，连接 $AD，BC$，线段 $AD$与 $BC$的数量关系是＿＿＿＿＿＿；

【类比迁移】

（2）如图2，将图1中的 $△COD$绕着点 $O$顺时针旋转 $\alpha （0°＜\alpha ＜90°）$，那么第（1）问的结论是否仍然成立？如果成立，证明你的结论；如果不成立，说明理由．

【方法运用】

（3）如图3，若 $AB＝8$，点 $C$是线段 $AB$外一动点， $AC＝3\sqrt{3}$，连接 $BC$．

①若将 $CB$绕点 $C$逆时针旋转 $90°$得到 $CD$，连接 $AD$，则 $AD$的最大值是＿＿＿＿＿＿；

②若以 $BC$为斜边作 $Rt△BCD$（ $B，C，D$三点按顺时针排列）， $\angle CDB＝90°$，连接 $AD$，当 $\angle CBD＝\angle DAB＝30°$时，直接写出 $AD$的值．

抛物线的解析式是 $y＝﹣x^2+4x+a$．直线 $y＝﹣x+2$与 $x$轴交于点 $M$，与 $y$轴交于点 $E$，点 $F$与直线上的点 $G（5，﹣3）$关于 $x$轴对称．

（1）如图①，求射线 $MF$的解析式；

（2）在（1）的条件下，当抛物线与折线EMF有两个交点时，设两个交点的横坐标是 $x_1$， $x_2（x_1＜x_2）$，求 $x_1+x_2$的值；

（3）如图②，当抛物线经过点 $C（0，5）$时，分别与 $x$轴交于 $A，B$两点，且点 $A$在点 $B$的左侧．在 $x$轴上方的抛物线上有一动点 $P$，设射线 $AP$与直线 $y＝﹣x+2$交于点 $N$．求 $\frac{\mathrm{PN}}{\mathrm{AN}}$的最大值．

已知正方形ABCD，E为对角线AC上一点．

【建立模型】

（1）如图1，连接BE，DE．求证： $BE＝DE$；

【模型应用】

（2）如图2，F是DE延长线上一点， $FB\perp BE$，EF交AB于点G．

①判断△FBG的形状并说明理由；

②若G为AB的中点，且AB＝4，求AF的长．

【模型迁移】

（3）如图3，F是DE延长线上一点， $FB\perp BE$，EF交AB于点G， $BE＝BF$．求证： $GE＝（\sqrt{2}-1）DE$．

如图，在菱形 $ABCD$中， $\angle BAD＝120°$， $AB＝6$，连接 $BD$．

（1）求 $BD$的长；

（2）点E为线段 $BD$上一动点（不与点B，D重合），点 $F$在边 $AD$上，且 $BE=\sqrt{3}DF$．

①当 $CE\perp AB$时，求四边形 $ABEF$的面积；

②当四边形 $ABEF$的面积取得最小值时， $CE+\sqrt{3}CF$的值是否也最小？如果是，求 $CE+\sqrt{3}CF$的最小值；如果不是，请说明理由．

已知直线 $l：y＝kx+b$经过点 $（0,7）$和点 $（1,6）$．

（1）求直线 $l$的解析式；

（2）若点 $P（m,n）$在直线l上，以P为顶点的抛物线G过点 $（0,﹣3）$，且开口向下．

①求m的取值范围；

②设抛物线G与直线l的另一个交点为Q，当点Q向左平移1个单位长度后得到的点 $Q\prime$也在G上时，求G在 $\frac{4m}{5}\le x\le \frac{4m}{5}+1$的图象的最高点的坐标．

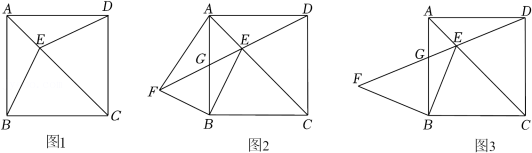
某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度．如图，在某一时刻，旗杆AB的影子为BC，与此同时在C处立一根标杆CD，标杆CD的影子为CE， $CD＝1.6m,BC＝5CD$．

（1）求 $BC$的长；

（2）从条件①、条件②这两个条件中选择一个作为已知，求旗杆AB的高度．

条件①： $CE＝1.0m$；条件②：从D处看旗杆顶部A的仰角 $\alpha$为 $54.46°$．

注：如果选择条件①和条件②分别作答，按第一个解答计分．

参考数据： $\sin 54.46°\approx 0.81,\cos 54.46°\approx 0.58,\tan 54.46°\approx 1.40$．

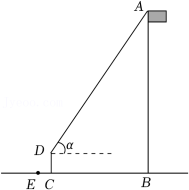
如图，AB是⊙O的直径，点C在⊙O上，且 $AC＝8,BC＝6$．

（1）尺规作图：过点O作AC的垂线，交劣弧 $\widehat{\mathit{AC}}$于点D，连接CD（保留作图痕迹，不写作法）；

（2）在（1）所作的图形中，求点O到AC的距离及 $\sin \angle ACD$的值．

在平面直角坐标系 $xOy$中，已知抛物线 $y＝a{x}^2+bx$经过 $A（4,0）,B（1,4）$两点． $P$是抛物线上一点，且在直线 $AB$的上方．

（1）求抛物线的解析式；

（2）若 $△OAB$面积是 $△PAB$面积的2倍，求点 $P$的坐标；

（3）如图， $OP$交 $AB$于点 $C$， $PD\parallel BO$交 $AB$于点 $D$．记 $△CDP$， $△CPB$, $△CBO$的面积分别为 $S_1,S_2,S_3$．判断 $\frac{S_1}{S_2}+\frac{S_2}{S_3}$是否存在最大值．若存在，求出最大值；若不存在，请说明理由．

已知 $△ABC≌△DEC$， $AB＝AC$， $AB＞BC$．

（1）如图1， $CB$平分 $\angle ACD$，求证：四边形 $ABDC$是菱形；

（2）如图2，将（1）中的 $△CDE$绕点 $C$逆时针旋转（旋转角小于 $\angle BAC$）， $BC,DE$的延长线相交于点 $F$，用等式表示 $\angle ACE$与 $\angle EFC$之间的数量关系，并证明；

（3）如图3，将（1）中的 $△CDE$绕点 $C$顺时针旋转（旋转角小于 $\angle ABC$），若 $\angle BAD＝\angle BCD$，求 $\angle ADB$的度数．