如图,已知圆内接四边形 的对角线 交于点 ,点 在对角线 上,且满足 .求证:
(1) 为 的中点;
(2) .

点 到图形 (可以是线段、三角形、圆或不规则图形等)的距离是指点 与图形 中所有点连接的线段中最短线段的长度.如图①中的两个虚线段 的长度都表示点 到图形 的距离.
如图②,在平面直角坐标系 中, 的三个顶点坐标分别为 ,点 从原点出发,以每秒 个单位长度的速度向 轴的正方向运动了 .
(1)当 时,求点 到 的距离;
(2)当点 到 的距离等于线段 的长度时,求 的取值范围;
(3)当点 到 的距离大于 时,求 的取值范围.

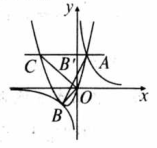
如图抛物线 与双曲线 有公共点 ,已知点 的坐标为 ,点 在第三象限内,且 的面积为 ( 为坐标原点).
(1)求实数 的值;
(2)过抛物线上点 作直线 轴,交拋物线于另一点 ,求所有满足 的点 的坐标.
已知直线 上点 ,过点 作 轴交 轴于点 ,交双曲线 于点 ,过点 作 轴交 轴于点 ,交双曲线 于点 ,若 是 的中点,且四边形 的面积为 .
(1)求 的值;
(2)若 是双曲线 第一象限上的任一点,求证: 为常数6;
(3)现在双曲线 上选一处 建一座码头,向 两地转运货物,经测算,从 到 ,从 到 修建公路的费用都是每单位长度 万元,则码头 应建在何处,才能使修建两条公路的总费用最低?(提示:利用(2)的结论转化)
一场数学游戏在两个非常聪明的学生甲、乙之间进行.裁判先在黑板上写出下面的正整数 ,然后随意擦去一个数.接下来由乙、甲两人轮流擦去其中的一个数(即乙先擦去其中的一个数,然后甲再擦去一个数,如此轮流下去),若最后剩下的两个数互质,则判甲胜;否则,判乙胜.
按照这种游戏规则,求甲获胜的概率(用具体的数字作答).
已知矩形 中, .点 是 边上一动点,连接 ,以 为直径作 ,交 于点 ,过点 作于 于点 .
(1)当直线 与 相切时,求 的长;
(2)当 时,求 的长;
(3)若线段 交 于点 ,在点 运动过程中, 能否成为等腰直角三角形?如果能,求出此时 的长,如果不能,说明理由.

如图, 是 的直径,过点 作 的切线 ,点 在右半圆上移动(点 与点 不重合),过点 作 ,垂足为 .点 在射线 上移动(点 在点 的右边),且在移动过程中保持 .
(1)若 的延长线相交于点 ,判断是否存在点 ,使得点 恰好在 上?若存在,求出 的大小;若不存在,请说明理由;
(2)连接 交 于点 ,设 ,试问: 的值是否随点 的移动而变化?证明你的结论.

如图,在平行四边形 中, 为对角线 上一点,且满足 的延长线与 的外接圆交于点 ,证明: .

已知两个不相等的实数 满足 ,且 .
(1)求 的值;
(2)已知自变量为 的函数 交 轴交于不同的两点 ,函数图象的顶点为 ,若 是等边三角形,求 的值;
(3)已知自变量为 的函数 ,当 时,总有 成立,求 的取值范围.
甲、乙两汽车出租公司均有50辆汽车对外出租,下面是两公司经理的一段对话:
甲公司经理:如果我公司每辆汽车月租费 元,那么 辆汽车可以全部租出.如果每辆汽车的月租费每增加 元,那么将少租出1辆汽车.另外,公司为每辆租出的汽车支付月维护费 元.
乙公司经理:我公司每辆汽车月租费 元,无论是否租出汽车,公司均需一次性支付月维护费共计 元.
说明:①汽车数量为整数;②月利润=月租车费-月维护费;③两公司月利润差=月利润较高公司的利润-月利润较低公司的利润.
在两公司租出的汽车数量相等的条件下,根据上述信息,解决下列问题:
(1)当每个公司租出的汽车为 辆时,甲公司的月利润是____元;当每个公司租出的汽车为____辆时,两公司的月利润相等;
(2)求两公司月利润差的最大值;
(3)甲公司热心公益事业,每租出 辆汽车捐出 元 给慈善机构,如果捐款后甲公司剩余的月利润仍高于乙公司月利润,且当两公司租出的汽车均为 辆时,甲公司剩余的月利润与乙公司月利润之差最大,求 的取值范围.
已知 的两边 的长是关于 的一元二次方程 的两个实数根,第三边 .
(1) 为何值时, 是以 为斜边的直角三角形?
(2) 为何值时, 是等腰三角形?并求此时 的周长.