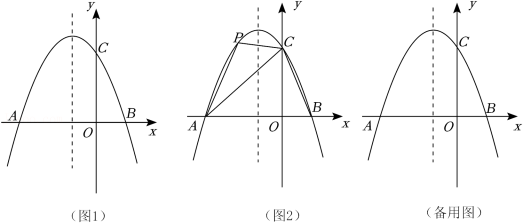
在平面直角坐标系中,点 是坐标原点,抛物线 经过点 ,对称轴为直线 .
(1)求 的值;
(2)已知点 在抛物线上,点 的横坐标为 ,点 的横坐标为 .过点 作 轴的垂线交直线 于点 ,过点 作 轴的垂线交直线 于点 .
(i)当 时,求 与 的面积之和;
(ii)在抛物线对称轴右侧,是否存在点 ,使得以 为顶点的四边形的面积为 ?若存在,请求出点 的横坐标 的值;若不存在,请说明理由.
综合运用
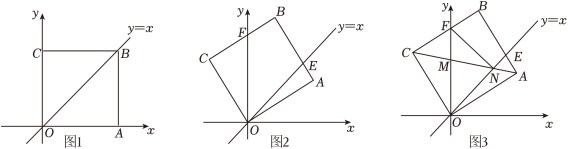
如图1,在平面直角坐标系中,正方形 的顶点 在 轴的正半轴上.如图2,将正方形 绕点 逆时针旋转,旋转角为 , 交直线 于点 , 交 轴于点 .
(1)当旋转角 为多少度时, ;(直接写出结果,不要求写解答过程)
(2)若点 ,求 的长;
(3)如图3,对角线 交 轴于点 ,交直线 于点 ,连接 .将 与 的面积分别记为 与 .设 , ,求 关于 的函数表达式.
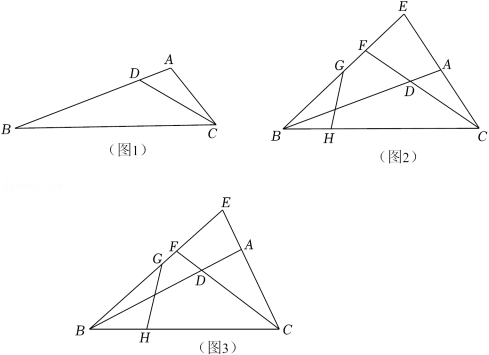
如图,在锐角△ABC中, ,点D,E分别是边AB,AC上一动点,连接BE交直线CD于点F.
(1)如图1,若 ,且 , ,求 的度数;
(2)如图2,若 ,且 ,在平面内将线段AC绕点C顺时针方向旋转60°得到线段CM,连接MF,点N是MF的中点,连接CN.在点D,E运动过程中,猜想线段BF,CF,CN之间存在的数量关系,并证明你的猜想;
(3)若 ,且 ,将 沿直线AB翻折至 所在平面内得到 ,点H是AP的中点,点K是线段PF上一点,将 沿直线HK翻折至 所在平面内得到 ,连接PQ.在点D,E运动过程中,当线段PF取得最小值,且 时,请直接写出 的值.

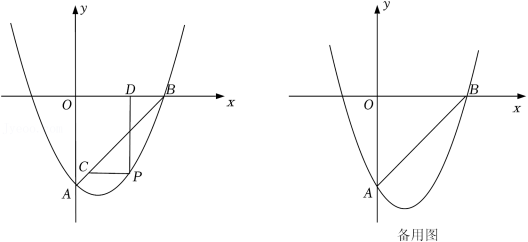
如图,在平面直角坐标系中,抛物线 与直线AB交于点 , .
(1)求该抛物线的函数表达式;
(2)点P是直线AB下方抛物线上的一动点,过点P作 轴的平行线交AB于点C,过点P作 轴的平行线交 轴于点D,求 的最大值及此时点P的坐标;
(3)在(2)中 取得最大值的条件下,将该抛物线沿水平方向向左平移5个单位,点E为点P的对应点,平移后的抛物线与 轴交于点F,M为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点N,使得以点E,F,M,N为顶点的四边形是平行四边形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.
若一个四位数M的个位数字与十位数字的平方和恰好是M去掉个位与十位数字后得到的两位数,则这个四位数M为“勾股和数”.
例如: ,∵ ,∴2543是“勾股和数”;
又如: ,∵ , ,∴4325不是“勾股和数”.
(1)判断2022,5055是否是“勾股和数”,并说明理由;
(2)一个“勾股和数”M的千位数字为a,百位数字为b,十位数字为c,个位数字为d,记 , .当 , 均是整数时,求出所有满足条件的M.
在平面直角坐标系中,抛物线 与 轴相交于点 (点 在点 的左侧),与 轴相交于点 ,连接 .
(1)求点 ,点 的坐标;
(2)如图1,点 在线段 上(点 不与点 重合),点 在 轴负半轴上, ,连接 ,设 的面积为 , 的面积为 , ,当 取最大值时,求 的值;
(3)如图2,抛物线的顶点为 ,连接 ,点 在第一象限的抛物线上, 与 相交于点 ,是否存在点 ,使 ,若存在,请求出点P的坐标;若不存在,请说明理由.
综合与实践
问题情境:数学活动课上,王老师出示了一个问题:
如图1,在 中, 是 上一点, .求证 .
独立思考:(1)请解答王老师提出的问题.
实践探究:(2)在原有问题条件不变的情况下,王老师增加下面的条件,并提出新问题,请你解答.
“如图2,延长 至点 ,使 , 与 的延长线相交于点 ,点 分别在 上, .在图中找出与 相等的线段,并证明.”
问题解决:(3)数学活动小组同学对上述问题进行特殊化研究之后发现,当 时,若给出 中任意两边长,则图3中所有已经用字母标记的线段长均可求.该小组提出下面的问题,请你解答.
“如图3,在(2)的条件下,若 ,求 的长.”
如图,矩形 中, , 是 边上一点(不与点 重合),作 于 , 于 ,延长 至点 ,使 ,连接 .
(1)直接写出图中与 相似的一个三角形;
(2)若四边形 是平行四边形,求 的长;
(3)当 的长为多少时,以 为顶点的三角形是以 为腰的等腰三角形?

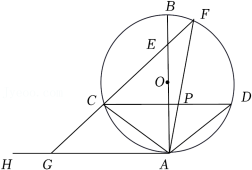
如图,以 为直径的 与 相切于点 ,点 在 左侧圆弧上,弦 交 于点 ,连结 .点 关于 的对称点为 ,直线 交 于点 ,交 于点 .
(1)求证: ;
(2)当点 在 上,连结 交 于点 ,若 ,求 的值;
(3)当点 在射线 上, ,以点 为顶点的四边形中有一组对边平行时,求 的长.
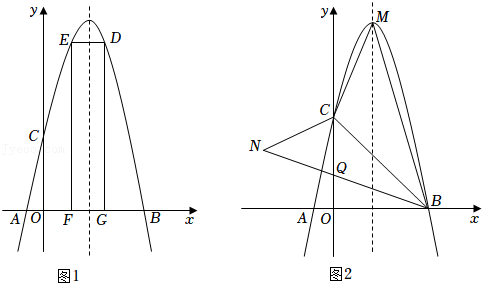
如图,已知点 在二次函数 的图象上,且 .
(1)若二次函数的图象经过点 .
①求这个二次函数的表达式;
②若 ,求顶点到 的距离;
(2)当 时,二次函数的最大值与最小值的差为 ,点 在对称轴的异侧,求 的取值范围.

如图1,四边形 中, , 于点 .将 与该四边形按如图方式放在同一平面内,使点 与 重合,点 在 上,其中 .

(1)求证: ;
(2) 从图1的位置出发,先沿着 方向向右平移(图2),当点 到达点 后立刻绕点 逆时针旋转(图3),当边 旋转 时停止.
①边 从平移开始,到绕点 旋转结束,求边 扫过的面积;
②如图2,点 在 上,且 .若 右移的速度为每秒 个单位长,绕点 旋转的速度为每秒 ,求点 在 区域(含边界)内的时长;
③如图3,在 旋转过程中,设 分别交 于点 ,若 ,直接写出 的长(用含 的式子表示).
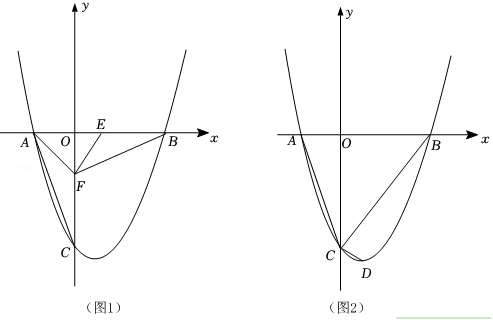
已知抛物线 与 轴交于 两点,与 轴交于点 .
(1)求 的值;
(2)如图1,点 是抛物线上位于对称轴右侧的一个动点,且点 在第一象限内,过点 作 轴的平行线交抛物线于点 ,作 轴的平行线交 轴于点 ,过点 作 轴,垂足为点 ,当四边形 的周长最大时,求点 的坐标;
(3)如图2,点 是抛物线的顶点,将 沿 翻折得到 , 与 轴交于点 ,在对称轴上找一点 ,使得 是以 为直角边的直角三角形,求出所有符合条件的点 的坐标.
如图,在四边形 中,对角线 与 相交于点 ,记 的面积为 , 的面积为 .
(1)问题解决:如图①,若 ,求证:
(2)探索推广:如图②,若 与 不平行,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
(3)拓展应用:如图③,在 上取一点 ,使 ,过点 作 交 于点 ,点 为 的中点, 交 于点 ,且 ,若 ,求 值.

如图1,平面直角坐标系 中,抛物线 与 轴分别交于点 和点 ,与 轴交于点 ,对称轴为直线 ,且 , 为抛物线上一动点.
(1)直接写出抛物线的解析式;
(2)如图2,连接 ,当点 在直线 上方时,求四边形 面积的最大值,并求出此时 点的坐标;
(3)设M为抛物线对称轴上一动点,当 运动时,在坐标轴上是否存在点 ,使四边形 为矩形?若存在,直接写出点 及其对应点 的坐标;若不存在,请说明理由.