已知矩形 中, .点 是 边上一动点,连接 ,以 为直径作 ,交 于点 ,过点 作于 于点 .
(1)当直线 与 相切时,求 的长;
(2)当 时,求 的长;
(3)若线段 交 于点 ,在点 运动过程中, 能否成为等腰直角三角形?如果能,求出此时 的长,如果不能,说明理由.
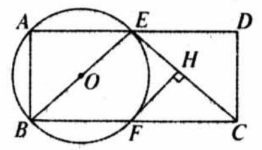
已知矩形 中, .点 是 边上一动点,连接 ,以 为直径作 ,交 于点 ,过点 作于 于点 .
(1)当直线 与 相切时,求 的长;
(2)当 时,求 的长;
(3)若线段 交 于点 ,在点 运动过程中, 能否成为等腰直角三角形?如果能,求出此时 的长,如果不能,说明理由.
