如图,已知抛物线 与 轴交于 两点,与 轴交于点 ,点 为抛物线的顶点.
(1)求抛物线的函数表达式及点 的坐标;
(2)若四边形 为矩形, .点 以每秒 个单位的速度从点 沿 向点 运动,同时点 以每秒 个单位的速度从点 沿 向点 运动,一点到达终点,另一点随之停止.当以 为顶点的三角形与 相似时,求运动时间 的值;
(3)抛物线的对称轴与 轴交于点 ,点 是点 关于点 的对称点,点 是 轴下方抛物线上的动点.若过点 的直线 与抛物线只有一个公共点,且分别与线段 相交于点 ,求证: 为定值.
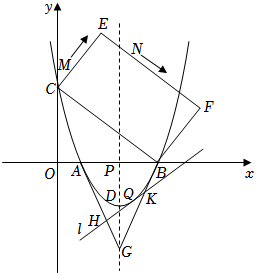
如图,已知抛物线 与 轴交于 两点,与 轴交于点 ,点 为抛物线的顶点.
(1)求抛物线的函数表达式及点 的坐标;
(2)若四边形 为矩形, .点 以每秒 个单位的速度从点 沿 向点 运动,同时点 以每秒 个单位的速度从点 沿 向点 运动,一点到达终点,另一点随之停止.当以 为顶点的三角形与 相似时,求运动时间 的值;
(3)抛物线的对称轴与 轴交于点 ,点 是点 关于点 的对称点,点 是 轴下方抛物线上的动点.若过点 的直线 与抛物线只有一个公共点,且分别与线段 相交于点 ,求证: 为定值.
