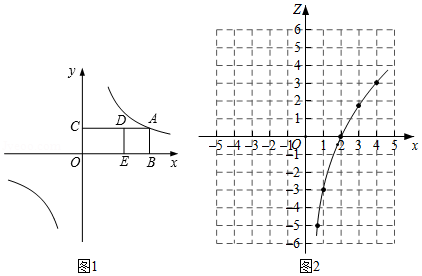
如图1是一座抛物线型拱桥侧面示意图.水面宽 与桥长 均为 ,在距离 点6米的 处,测得桥面到桥拱的距离 为 ,以桥拱顶点 为原点,桥面为 轴建立平面直角坐标系.
(1)求桥拱顶部 离水面的距离.
(2)如图2,桥面上方有3根高度均为 的支柱 , , ,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为 .
①求出其中一条钢缆抛物线的函数表达式.
②为庆祝节日,在钢缆和桥拱之间竖直装饰若干条彩带,求彩带长度的最小值.
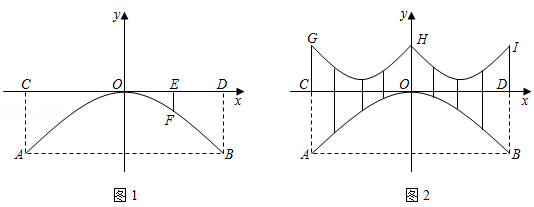
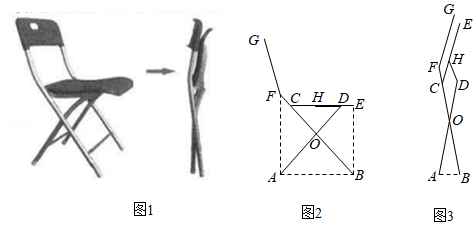
图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面 与地面平行,支撑杆 , 可绕连接点 转动,且 ,椅面底部有一根可以绕点 转动的连杆 ,点 是 的中点, , 均与地面垂直,测得 , , .
(1)椅面 的长度为 .
(2)如图3,椅子折叠时,连杆 绕着支点 带动支撑杆 , 转动合拢,椅面和连杆夹角 的度数达到最小值 时, , 两点间的距离为 (结果精确到 .
(参考数据: , ,
【证明体验】
(1)如图1, 为 的角平分线, ,点 在 上, .求证: 平分 .
【思考探究】
(2)如图2,在(1)的条件下, 为 上一点,连结 交 于点 .若 , , ,求 的长.
【拓展延伸】
(3)如图3,在四边形 中,对角线 平分 , ,点 在 上, .若 , , ,求 的长.

如图,在矩形 中,点 在边 上, 与 关于直线 对称,点 的对称点 在边 上, 为 中点,连结 分别与 , 交于 , 两点.若 , ,则 的长为 , 的值为 .

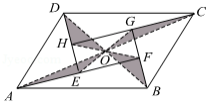
如图是一个由5张纸片拼成的平行四边形 ,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为 ,另两张直角三角形纸片的面积都为 ,中间一张矩形纸片 的面积为 , 与 相交于点 .当 , , , 的面积相等时,下列结论一定成立的是
| A. |
|
B. |
|
C. |
|
D. |
|
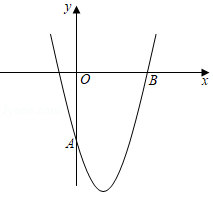
如图,已知抛物线 经过点 , .
(1)求 , 的值;
(2)连结 ,交抛物线 的对称轴于点 .
①求点 的坐标;
②将抛物线 向左平移 个单位得到抛物线 .过点 作 轴,交抛物线 于点 . 是抛物线 上一点,横坐标为 ,过点 作 轴,交抛物线 于点 ,点 在抛物线 对称轴的右侧.若 ,求 的值.
背景:点 在反比例函数 的图象上, 轴于点 , 轴于点 ,分别在射线 , 上取点 , ,使得四边形 为正方形.如图1,点 在第一象限内,当 时,小李测得 .
探究:通过改变点 的位置,小李发现点 , 的横坐标之间存在函数关系.请帮助小李解决下列问题.
(1)求 的值.
(2)设点 , 的横坐标分别为 , ,将 关于 的函数称为" 函数".如图2,小李画出了 时" 函数"的图象.
①求这个" 函数"的表达式.
②补画 时" 函数"的图象,并写出这个函数的性质(两条即可).
③过点 作一直线,与这个" 函数"图象仅有一个交点,求该交点的横坐标.
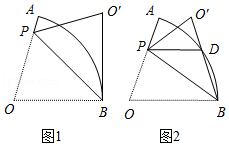
在扇形 中,半径 ,点 在 上,连结 ,将 沿 折叠得到△ .
(1)如图1,若 ,且 与 所在的圆相切于点 .
①求 的度数.
②求 的长.
(2)如图2, 与 相交于点 ,若点 为 的中点,且 ,求 的长.
如图1是一种根据镜面反射,放大微小变化的装置.木条 上的点 处安装一平面镜, 与刻度尺边 的交点为 ,从 点发出的光束经平面镜 反射后,在 上形成一个光点 .已知 , , , , .
(1) 的长为 .
(2)将木条 绕点 按顺时针方向旋转一定角度得到 (如图 ,点 的对应点为 , 与 的交点为 ,从 点发出的光束经平面镜 反射后,在 上的光点为 .若 ,则 的长为 .

已知二次函数 .
(1)求二次函数图象的顶点坐标;
(2)当 时,函数的最大值和最小值分别为多少?
(3)当 时,函数的最大值为 ,最小值为 ,若 ,求 的值.
如图,在 中, , , ,点 从点 出发沿 方向运动,到达点 时停止运动,连结 ,点 关于直线 的对称点为 ,连结 , .在运动过程中,点 到直线 距离的最大值是 ;点 到达点 时,线段 扫过的面积为 .

已知在 中, 是 的中点, 是 延长线上的一点,连结 , .

(1)如图1,若 , , , ,求 的长.
(2)过点 作 ,交 延长线于点 ,如图2所示,若 , ,求证: .
(3)如图3,若 ,是否存在实数 ,当 时, ?若存在,请写出 的值;若不存在,请说明理由.
由沈康身教授所著,数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图,三姐妹为了平分一块边长为1的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分).则图中 的长应是 .

已知抛物线 与 轴的交点为 和 ,点 , , , 是抛物线上不同于 , 的两个点,记△ 的面积为 ,△ 的面积为 ,有下列结论:①当 时, ;②当 时, ;③当 时, ;④当 时, .其中正确结论的个数是
| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |