【证明体验】
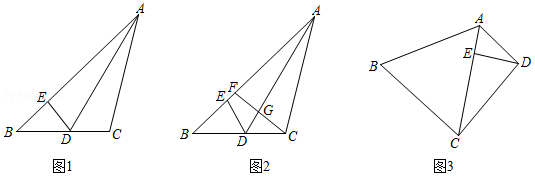
(1)如图1, 为 的角平分线, ,点 在 上, .求证: 平分 .
【思考探究】
(2)如图2,在(1)的条件下, 为 上一点,连结 交 于点 .若 , , ,求 的长.
【拓展延伸】
(3)如图3,在四边形 中,对角线 平分 , ,点 在 上, .若 , , ,求 的长.
相关知识点
推荐套卷
【证明体验】
(1)如图1, 为 的角平分线, ,点 在 上, .求证: 平分 .
【思考探究】
(2)如图2,在(1)的条件下, 为 上一点,连结 交 于点 .若 , , ,求 的长.
【拓展延伸】
(3)如图3,在四边形 中,对角线 平分 , ,点 在 上, .若 , , ,求 的长.
