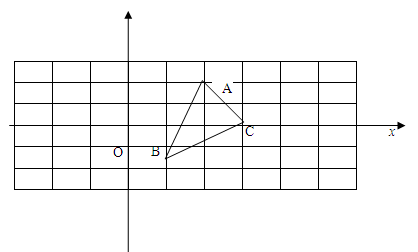
如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的三个顶点的坐标分别是：A（2，2），B（1，0），C（3，1）.
（1）画出△ABC关于x轴对称的△A’B’C’，并求出点A’、B’、C’的坐标.
|
（2）在坐标平面内是否存在点D，使得△COD为等腰三角形？若存在，直接写出点D的坐标（找出满足条件的两个点即可），若不存在，请说明理由.
相关试题
（如图），试取斜边
上的一点为圆心画图，使点
，
，
分别在所画的圆内、圆外和圆上．
，连结
，
相交于点
，以点
为圆心，
cm长为半径画圆，试判断点
，
，
，
中，
，求证
，
，
，
四个顶点共圆．推荐套卷
如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的三个顶点的坐标分别是：A（2，2），B（1，0），C（3，1）.
（1）画出△ABC关于x轴对称的△A’B’C’，并求出点A’、B’、C’的坐标.
|
（2）在坐标平面内是否存在点D，使得△COD为等腰三角形？若存在，直接写出点D的坐标（找出满足条件的两个点即可），若不存在，请说明理由.
粤公网安备 44130202000953号