设抛物线 ,其中 为实数.
(1)若抛物线经过点 ,则 ;
(2)将抛物线 向上平移2个单位,所得抛物线顶点的纵坐标的最大值是 .
在 中, ,分别过点 , 作 平分线的垂线,垂足分别为点 , , 的中点是 ,连接 , , .则下列结论错误的是
| A. |
|
B. |
|
C. |
|
D. |
|
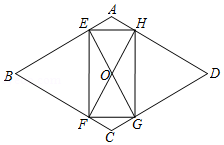
如图,在菱形 中, , ,过菱形 的对称中心 分别作边 , 的垂线,交各边于点 , , , ,则四边形 的周长为
| A. |
|
B. |
|
C. |
|
D. |
|
已知,在 中, , .

(1)如图1,已知点 在 边上, , ,连结 .试探究 与 的关系;
(2)如图2,已知点 在 下方, , ,连结 .若 , , , 交 于点 ,求 的长;
(3)如图3,已知点 在 下方,连结 、 、 .若 , , , ,求 的值.
如图,在菱形 中, , 交 的延长线于点 .连结 交 于点 ,交 于点 . 于点 ,连结 .有下列结论:① ;② ;③ ;④ .其中所有正确结论的序号为 .

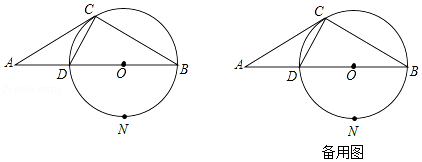
如图1, 为 上一点,点 在直径 的延长线上,且 .
(1)判断直线 与 的位置关系,并说明理由;
(2)若 , ,求 的半径;
(3)如图2,在(2)的条件下, 的平分线 交 于点 ,交 于点 ,连结 .求 的值.

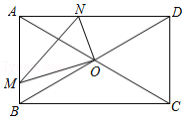
如图,在矩形 中, ,对角线相交于点 ,动点 从点 向点 运动(到点 即停止),点 是 上一动点,且满足 ,连结 .在点 、 运动过程中,则以下结论正确的是 .(写出所有正确结论的序号)
①点 、 的运动速度不相等;
②存在某一时刻使 ;
③ 逐渐减小;
④ .
如图,在 中, 是直径, 是弦, ,垂足为 ,过点 的 的切线与 延长线交于点 ,连接 .
(1)求证: 为 的切线;
(2)若 半径为3, ,求 .

如图,在矩形 中, , 相交于点 ,过点 作 于点 ,交 于点 ,过点 作 交 于点 .交 于点 ,连接 , .有下列结论:①四边形 为平行四边形;② ;③ 为等边三角形;④当 时,四边形 是菱形.其中,正确结论的序号 .

如图, 的半径为1,点 是 的直径 延长线上的一点, 为 上的一点, , .
(1)求证:直线 是 的切线;
(2)求 的面积;
(3)点 在 上运动(不与 、 重合),过点 作 的垂线,与 的延长线交于点 .
①当点 运动到与点 关于直径 对称时,求 的长;
②当点 运动到什么位置时, 取到最大值,并求出此时 的长.
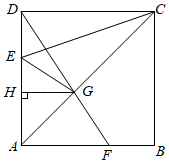
如图,正方形 中,点 是 边上一点,连结 ,以 为对角线作正方形 ,边 与正方形 的对角线 相交于点 ,连结 ,有以下五个结论:
① ;
② ;
③ ;
④ ;
⑤若 ,则 .
你认为其中正确是 .(填写序号)

如图,点 在正方形 边 上,点 是线段 上的动点(不与点 重合), 交 于点 , 于点 , , .
(1)求 ;
(2)设 , ,试探究 与 的函数关系式(写出 的取值范围);
(3)当 时,判断 与 的位置关系并说明理由.
超市购进某种苹果,如果进价增加2元 千克要用300元;如果进价减少2元 千克,同样数量的苹果只用200元.
(1)求苹果的进价;
(2)如果购进这种苹果不超过100千克,就按原价购进;如果购进苹果超过100千克,超过部分购进价格减少2元 千克,写出购进苹果的支出 (元 与购进数量 (千克)之间的函数关系式;
(3)超市一天购进苹果数量不超过300千克,且购进苹果当天全部销售完,据统计,销售单价 (元 千克)与一天销售数量 (千克)的关系为 .在(2)的条件下,要使超市销售苹果利润 (元 最大,求一天购进苹果数量.(利润 销售收入 购进支出)
如图,在矩形 中, , ,把边 沿对角线 平移,点 , 分别对应点 , 给出下列结论:
①顺次连接点 , , , 的图形是平行四边形;
②点 到它关于直线 的对称点的距离为48;
③ 的最大值为15;
④ 的最小值为 .
其中正确结论的个数是

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |