本题满分分 已知函数f (x)=x3+ (1-a)x2-3ax+1,a>0.
(1-a)x2-3ax+1,a>0.
(Ⅰ) 证明:对于正数a,存在正数p,使得当x∈[0,p]时,有-1≤f (x)≤1;
(Ⅱ) 设(Ⅰ)中的p的最大值为g(a),求g(a)的最大值.
(本小题满分14分)
已知函数
(Ⅰ)若函数 处取得极值,求实数a的值;
处取得极值,求实数a的值;
(Ⅱ)在(I)条件下,若直线 与函数
与函数 的图象相切,求实数k的值;
的图象相切,求实数k的值;
(Ⅲ)记 ,求满足条件的实数a的集合.
,求满足条件的实数a的集合.
(本小题满分16分)
已知函数 ,若
,若 为定义在R上的奇函数,则(1)求实数
为定义在R上的奇函数,则(1)求实数 的值;(2)求函数
的值;(2)求函数 的值域;(3)求证:
的值域;(3)求证: 在R上为增函数;(4)若m为实数,解关于
在R上为增函数;(4)若m为实数,解关于 的不等式:
的不等式:
已知 其中
其中 .(1)求函数
.(1)求函数 的单调区间;(2)若函数
的单调区间;(2)若函数 在区间
在区间 内恰有两个零点,求
内恰有两个零点,求 的取值范围;
的取值范围;
(3)当 时,设函数
时,设函数 在区间
在区间 上的最大值为
上的最大值为 最小值为
最小值为 ,记
,记 ,求函数
,求函数 在区间
在区间 上的最小值.
上的最小值.
(本小题满分8分)已知函数 .
.
(1)求证:函数 在
在 上为增函数;
上为增函数;
(2)当函数 为奇函数时,求
为奇函数时,求 的值;
的值;
(3)当函数 为奇函数时, 求函数
为奇函数时, 求函数 在
在 上的值域.
上的值域.
(本小题满分14分)
设函数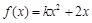 (
(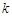 为实常数)为奇函数,函数
为实常数)为奇函数,函数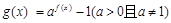 .
.
(Ⅰ)求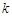 的值;
的值;
(Ⅱ)求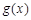 在
在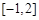 上的最大值;
上的最大值;
(Ⅲ)当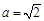 时,
时,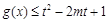 对所有的
对所有的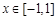 及
及 恒成立,求实数
恒成立,求实数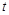 的取值范围.
的取值范围.
(本小题满分12分)
某种产品投放市场以来,通过市场调查,销量t(单位:吨)与利润Q(单位:万元)的变化关系如右表,现给出三种函数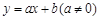 ,
,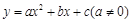 ,
,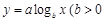 且
且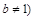 ,请你根据表中的数据,选取一个恰当的函数,使它能合理描述产品利润Q与销量t的变化,求所选取的函数的解析式,并求利润最大时的销量.
,请你根据表中的数据,选取一个恰当的函数,使它能合理描述产品利润Q与销量t的变化,求所选取的函数的解析式,并求利润最大时的销量.
| 销量t |
1 |
4 |
6 |
| 利润Q |
2 |
5 |
4.5 |
已知函数
(1)如果函数 的单调减区间为
的单调减区间为 ,求函数
,求函数 的解析式;
的解析式;
(2)在(1)的条件下,求函数 的图像过点
的图像过点 的切线方程;
的切线方程;
(3)证明:对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(12分)我们把同时满足下列两个性质的函数称为“和谐函数” :
①函数在整个定义域上是单调增函数或单调减函数;
②在函数的定义域内存在区间 ,使得函数在区间
,使得函数在区间 上的值域为
上的值域为 .
.
⑴已知幂函数 的图像经过点
的图像经过点 ,判断
,判断
 是否是和谐函数?
是否是和谐函数?
⑵判断函数 是否是和谐函数?
是否是和谐函数?
⑶若函数 是和谐函数,求实数
是和谐函数,求实数 的取值范围.
的取值范围.
已知函数
 的图像与
的图像与 轴有两个交点
轴有两个交点
(1)设两个交点的横坐标分别为 试判断函数
试判断函数 有没有最大值或最小值,并说明理由.
有没有最大值或最小值,并说明理由.
(2)若
 与
与 在区间
在区间 上都是减函数,求实数
上都是减函数,求实数 的取值范围.
的取值范围.
对于函数 ,若存在x0∈R,使方程
,若存在x0∈R,使方程 成立,则称x0为
成立,则称x0为 的不动点,已知函数
的不动点,已知函数 (a≠0).
(a≠0).
(1)当 时,求函数
时,求函数 的不动点;
的不动点;
(2)若对任意实数b,函数 恒有两个相异的不动点,求a的取值范围;
恒有两个相异的不动点,求a的取值范围;