高中数学函数迭代解答题

（本题12分）对于函数，若，则称为的“不动点”，若，则称为的“稳定点”，函数的“不动点”和“稳定点”的集合分别记为A和B，即．
（1）设，求集合A和B；
（2）若，，求实数的取值范围；

已知抛物线，
（1）用配方法确定它的顶点坐标、对称轴；
（2）取何值时，随增大而减小？
（3）取何值时，抛物线在轴上方？

已知，其中．
（1）当时，证明；
（2）若在区间，内各有一个根，求的取值范围

化循环小数为分数

已知函数在处取得极值.
（Ⅰ）求的解析式；
（Ⅱ）设是曲线上除原点外的任意一点,过的中点且垂直于轴的直线交曲线于点,试问：是否存在这样的点,使得曲线在点处的切线与平行？若存在,求出点的坐标；若不存在,说明理由；
（Ⅲ）设函数,若对于任意,总存在,使得,求实数的取值范围.

已知函数（为常数）．
（1）当时，求的单调递减区间；
（2）若，且对任意的，恒成立，求实数的取值范围.

函数
（1）时，求函数的单调区间;
（2）时，求函数在上的最大值.

已知函数，函数.
（1）判断函数的奇偶性；
（2）若当时，恒成立，求实数的最大值.

已知函数f(x)=-2alnx（a>0）
（I)求函数f（x）的单调区间和最小值.
（II）若方程f（x）=2ax有唯一解，求实数a的值.

设F（x）=3a+2bx+c，若a+b+c=0，且F（0）>0，F（1）>0.
求证：a>0，且—2<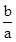<—1.

设定义在上的函数,满足当时,,且对任意,有,
（1）解不等式
（2）解方程

已知函数，,
(1)若为奇函数，求的值；
(2)若=1，试证在区间上是减函数；
(3)若=1，试求在区间上的最小值.

已知函数满足：（），
（1）用反证法证明：不可能为正比例函数；
（2）若，求的值，并用数学归纳法证明：对任意的，均有：.

已知函数是定义域为的奇函数，且当时，
，（。
（1）求实数的值；并求函数在定义域上的解析式；
（2）求证：函数上是增函数。

已知函数，若函数图象上任意一点关于原点的对称点的轨迹恰好是函数的图象.
（1）写出函数的解析式；
（2）当时总有成立，求的取值范围.