已知函数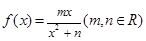 在
在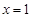 处取得极值
处取得极值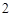 .
.
(Ⅰ)求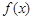 的解析式;
的解析式;
(Ⅱ)设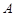 是曲线
是曲线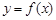 上除原点
上除原点 外的任意一点,过
外的任意一点,过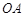 的中点且垂直于
的中点且垂直于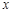 轴的直线交曲线于点
轴的直线交曲线于点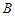 ,试问:是否存在这样的点
,试问:是否存在这样的点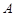 ,使得曲线在点
,使得曲线在点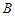 处的切线与
处的切线与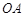 平行?若存在,求出点
平行?若存在,求出点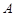 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(Ⅲ)设函数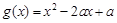 ,若对于任意
,若对于任意 ,总存在
,总存在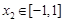 ,使得
,使得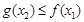 ,求实数
,求实数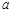 的取值范围.
的取值范围.
相关知识点
推荐套卷
已知函数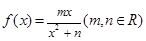 在
在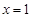 处取得极值
处取得极值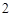 .
.
(Ⅰ)求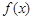 的解析式;
的解析式;
(Ⅱ)设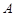 是曲线
是曲线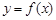 上除原点
上除原点 外的任意一点,过
外的任意一点,过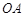 的中点且垂直于
的中点且垂直于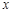 轴的直线交曲线于点
轴的直线交曲线于点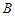 ,试问:是否存在这样的点
,试问:是否存在这样的点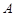 ,使得曲线在点
,使得曲线在点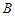 处的切线与
处的切线与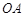 平行?若存在,求出点
平行?若存在,求出点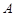 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(Ⅲ)设函数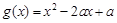 ,若对于任意
,若对于任意 ,总存在
,总存在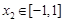 ,使得
,使得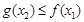 ,求实数
,求实数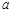 的取值范围.
的取值范围.