已知各项都不相等的等差数列 的前6项和为60,且
的前6项和为60,且 为
为 和
和 的等比中项.
的等比中项.
(1) 求数列 的通项公式;
的通项公式;
(2) 若数列 满足
满足 ,且
,且 ,求数列
,求数列 的前
的前 项和
项和 .
.
已知数列 满足
满足 ,
, ,
, ,
, 是数列
是数列 的前
的前 项和.
项和.
(1)若数列 为等差数列.
为等差数列.
①求数列的通项 ;
;
②若数列 满足
满足 ,数列
,数列 满足
满足 ,试比较数列
,试比较数列 前
前 项和
项和 与
与 前
前 项和
项和 的大小;
的大小;
(2)若对任意 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知数列 满足
满足 ,
, ,
, ,
, 是数列
是数列 的前
的前 项和.
项和.
(1)若数列 为等差数列.
为等差数列.
①求数列的通项 ;
;
②若数列 满足
满足 ,数列
,数列 满足
满足 ,试比较数列
,试比较数列 前
前 项和
项和 与
与 前
前 项和
项和 的大小;
的大小;
(2)若对任意 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知数列 中,
中,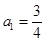 ,
,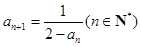 .
.
(1)求证:数列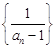 是等差数列,并求
是等差数列,并求 的通项公式;
的通项公式;
(2)设 ,
,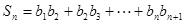 ,试比较
,试比较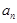 与
与 的大小.
的大小.
已知等比数列 中,
中, ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,
, 分别为等差数列
分别为等差数列 的第3项和第5项,试求数列
的第3项和第5项,试求数列 的通项公式及前
的通项公式及前 项和
项和 .
.
已知数列 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且 是
是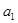 和
和 的等比中项.
的等比中项.
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为 ,
, ,试问当
,试问当 为何值时,
为何值时, 最大?并求出
最大?并求出 的最大值.
的最大值.
已知等差数列 满足:
满足: .
.
(Ⅰ)求 的通项公式及前
的通项公式及前 项和
项和 ;
;
(Ⅱ)若等比数列 的前
的前 项和为
项和为 ,且
,且 ,求
,求 .
.
设各项均为正数的数列 的前
的前 项和为
项和为 ,满足
,满足 且
且 恰好是等比数列
恰好是等比数列 的前三项.
的前三项.
(Ⅰ)求数列 、
、 的通项公式;
的通项公式;
(Ⅱ)记数列 的前
的前 项和为
项和为 ,若对任意的
,若对任意的 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
设各项均为正数的数列 的前
的前 项和为
项和为 ,满足
,满足 且
且 恰好是等比数列
恰好是等比数列 的前三项.
的前三项.
(Ⅰ)求数列 、
、 的通项公式;
的通项公式;
(Ⅱ)记数列 的前
的前 项和为
项和为 ,若对任意的
,若对任意的 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知首项为 的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)已知 ,求数列{bn}的前n项和
,求数列{bn}的前n项和 .
.
已知首项为 的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若 ,数列{bn}的前n项和Tn,求满足不等式
,数列{bn}的前n项和Tn,求满足不等式 ≥
≥ 的最大n值.
的最大n值.
已知集合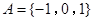 ,对于数列
,对于数列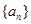 中
中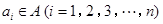 .
.
(Ⅰ)若三项数列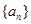 满足
满足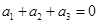 ,则这样的数列
,则这样的数列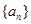 有多少个?
有多少个?
(Ⅱ)若各项非零数列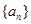 和新数列
和新数列 满足首项
满足首项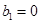 ,
,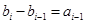 (
(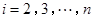 ),且末项
),且末项 ,记数列
,记数列 的前
的前 项和为
项和为 ,求
,求 的最大值.
的最大值.
设数列{an}满足an+1=2an+n2-4n+1.
(1)若a1=3,求证:存在 (a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;
(a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;
(2)若an是一个等差数列{bn}的前n项和,求首项a1的值与数列{bn}的通项公式.