如图, 是 的直径, 是弧 的中点,延长 至 ,使 ,连接 是 的中点, 的延长线交 的延长线于点 交 于点 ,连接 .
(1)求证: 是 的切线;
(2)若 ,求 的长.
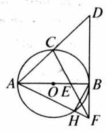
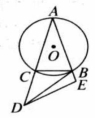
如图所示, 中, ,过点 作 的外接圆的切线交 的延长线于点 ,过点 作 交 的延长线于点 ,求证: .
等腰直角 和 如图放置,已知 的半径为 ,圆心 与直线 的距离为5,现 以每秒2个单位的速度向右移动,同时 的边长 又以每秒 个单位沿 方向增大.
(1)当 的边( 边除外)与圆第一次相切时,点 移动了多少距离?
(2)若 在移动的同时, 也以每秒 个单位的速度向右移动,则 从开始移动,到它的边与圆最后一次相切,一共经过了多少时间?
(3)在(2)条件下,是否存在某一时刻, 与 的公共部分等于 的面积?若存在,求出恰好符合条件时两个图形移动了多少时间?若不存在,请说明理由.

如图, 是 上两点,且 ,连接 并延长到点 ,使 ,连接 .
(1)求证: 是 的切线;
(2)点 分别是 的中点, 所在直线交 于点 ,求 的长.
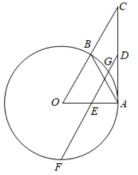
如图,在平行四边形 中, 为对角线 上一点,且满足 的延长线与 的外接圆交于点 ,证明: .

如图, 为 的直径,点 为 上异于 的一动点,弦 , 是关于 的一元二次方程 的两根,求 的最大值.

如图, 为 的垂心, 为 的外接圆.点 为以 为圆心, 长为半径的圆与 的交点, 为线段 的垂直平分线与 的交点.
求证:(1) 垂直平分线段 ;
(2) .

如图,已知在 中, 是 的外角平分线与 的外接圆的交点,点 在 上且 ,已知 ,求 的面积.

如图,点 是 的内心, ,过点 作一圆与边 相切于点 ,与直线 交于点 和点 ,连接 ,若 ,求 的大小.

已知 内接于 ,点 是 上一点.
(1)如图①,若 为 的直径,连接 ,求 和 的大小;
(2)如图②,若 ,连接 ,过点 作 的切线,与 的延长线交于点 ,求 的大小.
