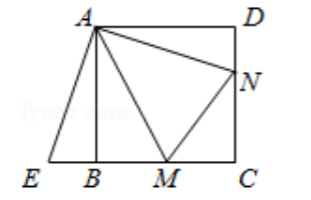
如图,点 , 分别在正方形 的边 , 上,且 ,把 绕点 顺时针旋转 得到 .
( 1 )求证: ≌ .
( 2 )若 , ,求正方形 的边长.
如图,圆 是 的外接圆,其切线 与直径 的延长线相交于点 ,且 .
( 1 )求 的度数;
( 2 )若 ,求圆 的半径.

通过课本上对函数的学习,我们积累了一定的经验,下表是一个函数的自变量 与函数值 的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:
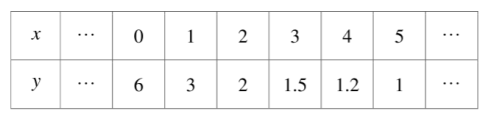
( 1 )当 时, ;
( 2 )根据表中数值描点 ,并画出函数图象;
( 3 )观察画出的图象,写出这个函数的一条性质: .
习近平总书记于 2019 年 8 月在兰州考察时说"黄河之滨也很美",兰州是古丝绸之路商贸重镇,也是黄河唯一穿城而过的省会城市,被称为"黄河之都",近年来,在市政府的积极治理下,兰州的空气质量得到极大改善,"兰州蓝"成为兰州市民引以为豪的城市名片,下图是根据兰州市环境保护局公布的 2013-2019 年各年的全年空气质量优良天数绘制的折线统计图.
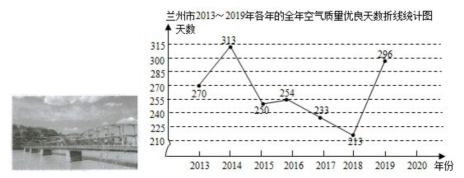
请结合统计图解答下列问题:
( 1 ) 2019 年比 2013 年的全年空气质量优良天数增加了 天;
( 2 )这七年的全年空气质量优良天数的中位数是 天;
( 3 )求这七年的全年空气质量优良天数的平均天数;
( 4 )《兰州市"十三五"质量发展规划》中指出: 2020 年,确保兰州市全年空气质量优良天数比率达 80% 以上,试计算 2020 年(共 366 天)兰州市空气质量优良天数至少需要多少天才能达标.
2019年甘肃在国际知名旅游指南《孤独星球》亚洲最佳旅游地排名第一,截至2020年1月,甘肃省已有五家国家5A级旅游景区,分别为A:嘉峪关文物景区;B:平凉崆峒山风景名胜区;C:天水麦积山景区;D:敦煌鸣沙月牙泉景区:E:张掖七彩舟霞景区,张帆同学与父母计划在暑假期间从中选择部分景区游玩.
(1)张帆一家选择E:张掖七彩丹霞景区的概率是多少?
(2)若张帆一家选择了E:张掖七彩丹霞景区,他们再从 , , , 四个景区中任选两个景区去旅游,求选 , 两个景区的概率(要求画树状图或列表求概率).
图①是甘肃省博物馆的镇馆之宝 -- 铜奔马,又称 " 马踏飞燕 " ,于 1969 年 10 月出土于武威市的雷台汉墓, 1983 年 10 月被国家旅游局确定为中国旅游标志,在很多旅游城市的广场上都有 " 马踏飞燕 " 雕塑,某学习小组把测量本城市广场的 " 马踏飞燕 " 雕塑(图②)最高点离地面的高度作为一次课题活动,同学们制定了测量方案,并完成了实地测量,测得结果如下表:
| 课题 |
测量 " 马踏飞燕 " 雕塑最高点离地面的高度 |
|||
| 测量示意图 |
|
如图,雕塑的最高点 到地面的高度为 ,在测点 用仪器测得点 的仰角为 ,前进一段距离到达测点 ,再用该仪器测得点 的仰角为 ,且点 , , , , , 均在同一竖直平面内,点 , , 在同一条直线上. |
||
| 测量数据 |
的度数 |
的度数 |
的长度 |
仪器 ( )的高度 |
|
|
|
5 米 |
米 |
|
请你根据上表中的测量数据,帮助该小组求出 " 马踏飞燕 " 雕塑最高点离地面的高度(结果保留一位小数).(参考数据: , , , , , )

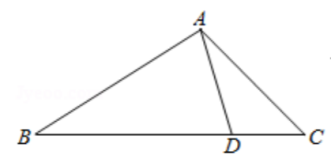
如图,在 中, 是 边上一点,且 .
( 1 )尺规作图(保留作图痕迹,不写作法)
①作 的角平分线交 于点 ;
②作线段 的垂直平分线交 于点 .
( 2 )连接 ,直接写出线段 和 的数量关系及位置关系.
(算一算)
如图 ① ,点 A 、 B 、 C 在数轴上, B 为 AC 的中点,点 A 表示 ,点 B 表示 1 ,则点 C 表示的数为 , AC 长等于 ;
(找一找)
如图②,点 M 、 N 、 P 、 Q 中的一点是数轴的原点,点 A 、 B 分别表示实数 、 , Q 是 AB 的中点,则点 是这个数轴的原点;
(画一画)
如图 ③ ,点 A 、 B 分别表示实数 、 ,在这个数轴上作出表示实数 n 的点 E (要求:尺规作图,不写作法,保留作图痕迹);
(用一用)
学校设置了若干个测温通道,学生进校都应测量体温,已知每个测温通道每分钟可检测 a 个学生.凌老师提出了这样的问题:假设现在校门口有 m 个学生,每分钟又有 b 个学生到达校门口.如果开放 3 个通道,那么用 4 分钟可使校门口的学生全部进校;如果开放 4 个通道,那么用 2 分钟可使校门口的学生全部进校.在这些条件下, a 、 m 、 b 会有怎样的数量关系呢?
爱思考的小华想到了数轴,如图 ④ ,他将 4 分钟内需要进校的人数 记作 ,用点 A 表示;将 2 分钟内由 4 个开放通道检测后进校的人数,即校门口减少的人数 记作 ,用点 B 表示.
① 用圆规在小华画的数轴上分别画出表示 、 的点 F 、 G ,并写出 的实际意义;
② 写出 a 、 m 的数量关系: .

如图, 中, 的平分线 交边 于点 , ,以点 为圆心, 长为半径作 ,分别交边 、 于点 、 .点 在边 上, 交 于点 , 为 的中点.
( 1 )求证:四边形 为菱形;
( 2 )已知 ,连接 ,当 与 相切时,求 的长.

如图,正比例函数 的图象与反比例函数 的图象交于点 和点 .
( 1 ) , ;
( 2 )点 在 轴正半轴上. ,求点 的坐标;
( 3 )点 在 x 轴上, 为锐角,直接写出 的取值范围.

如图,点 E 与树 AB 的根部点 A 、建筑物 CD 的底部点 C 在一条直线上, .小明站在点 E 处观测树顶 B 的仰角为 ,他从点 E 出发沿 EC 方向前进 到点 G 时,观测树顶 B 的仰角为 ,此时恰好看不到建筑物 CD 的顶部 D ( H 、 B 、 D 三点在一条直线上).已知小明的眼睛离地面 ,求建筑物 CD 的高度(结果精确到 ).(参考数据: , .)

智慧的中国古代先民发明了抽象的符号来表达丰富的含义.例如,符号"  "有刚毅的含义,符号"
"有刚毅的含义,符号"  "有愉快的含义.符号中的"
"有愉快的含义.符号中的"  "表示"阴","
"表示"阴","  "表示"阳",类似这样自上而下排成的三行符号还有其他的含义.所有这些三行符号中,每一行只有一个阴或一个阳,且出现阴、阳的可能性相同.
"表示"阳",类似这样自上而下排成的三行符号还有其他的含义.所有这些三行符号中,每一行只有一个阴或一个阳,且出现阴、阳的可能性相同.
( 1 )所有这些三行符号共有 种;
( 2 )若随机画一个这样的三行符号,求"画出含有一个阴和两个阳的三行符号"的概率.
教育部发布的义务教育质量监测结果报告显示,我国八年级学生平均每天的睡眠时间达 9 小时及以上的比例为 .某校数学社团成员采用简单随机抽样的方法,抽取了本校八年级 50 名学生,对他们一周内平均每天的睡眠时间 t (单位:小时)进行了调查,将数据整理后绘制成下表:
| 平均每天的睡眠时间分组 |
|
|
|
|
9 小时及以上 |
| 频数 |
|
|
|
|
|
该样本中学生平均每天的睡眠时间达 9 小时及以上的比例高于全国的这项数据,达到了 .
( 1 )求表格中 n 的值;
( 2 )该校八年级共 400 名学生,估计其中平均每天的睡眠时间在 这个范围内的人数是多少.