如图,点 E 与树 AB 的根部点 A 、建筑物 CD 的底部点 C 在一条直线上, .小明站在点 E 处观测树顶 B 的仰角为 ,他从点 E 出发沿 EC 方向前进 到点 G 时,观测树顶 B 的仰角为 ,此时恰好看不到建筑物 CD 的顶部 D ( H 、 B 、 D 三点在一条直线上).已知小明的眼睛离地面 ,求建筑物 CD 的高度(结果精确到 ).(参考数据: , .)
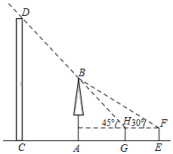
如图,点 E 与树 AB 的根部点 A 、建筑物 CD 的底部点 C 在一条直线上, .小明站在点 E 处观测树顶 B 的仰角为 ,他从点 E 出发沿 EC 方向前进 到点 G 时,观测树顶 B 的仰角为 ,此时恰好看不到建筑物 CD 的顶部 D ( H 、 B 、 D 三点在一条直线上).已知小明的眼睛离地面 ,求建筑物 CD 的高度(结果精确到 ).(参考数据: , .)
