如图,一次函数 与反比例函数 在第一象限交于 、N两点,NA垂直x轴于点A,O为坐标原点,四边形OANM的面积为 .
(1)求反比例函数及一次函数的解析式;
(2)点P是反比例函数第三象限内的图象上一动点,请简要描述使△PMN的面积最小时点P的位置(不需证明),并求出点P的坐标和△PMN面积的最小值.

某水果经营户从水果批发市场批发水果进行零售,部分水果批发价格与零售价格如下表:
水果品种 |
梨子 |
菠萝 |
苹果 |
车厘子 |
批发价格(元/kg) |
4 |
5 |
6 |
40 |
零售价格(元/kg) |
5 |
6 |
8 |
50 |
请解答下列问题:
(1)第一天,该经营户用 元批发了菠萝和苹果共 ,当日全部售出,求这两种水果获得的总利润?
(2)第二天,该经营户依然用 元批发了菠萝和苹果,当日销售结束清点盘存时发现进货单丢失,只记得这两种水果的批发量均为正整数且菠萝的进货量不低于 ,这两种水果已全部售出且总利润高于第一天这两种水果的总利润,请通过计算说明该经营户第二天批发这两种水果可能的方案有哪些?
目前,全球淡水资源分布不均、总量不足是人类面临的共同问题.某市在实施居民用水定额管理前,通过简单随机抽样对居民生活用水情况进行了调查,获得了若干个家庭去年的月均用水量数据(单位:t),整理出了频数分布表,频数分布直方图和扇形统计图,部分信息如下:
月均用水量(t) |
|
|
|
|
|
频数 |
|
|
|||
对应的扇形区域 |
A |
B |
C |
D |
E |
根据以上信息,解答下列问题:
(1)补全频数分布直方图,并求出扇形图中扇形E对应的圆心角的度数;
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使该市60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?并说明理由.


在 中, , , 是 的中点. 为直线 上一动点,连接 ,过点 作 ,交直线 于点 ,连接 .

( 1 )如图 1 ,当 是线段 的中点时,设 , ,求 的长(用含 的式子表示);
( 2 )当点 在线段 的延长线上时,依题意补全图 2 ,用等式表示线段 , , 之间的数量关系,并证明.
在平面直角坐标系 中, 为抛物线 上任意两点,其中 .
(1)若抛物线的对称轴为 ,当 为何值时,
(2)设抛物线的对称轴为 .若对于 ,都有 ,求 的取值范围.
小云统计了自己所住小区 5 月 1 日至 30 日的厨余垃圾分出量(单位:千克),相关信息如下:
.小云所住小区 5 月 1 日至 30 日的厨余垃圾分出量统计图:

.小云所住小区 5 月 1 日至 30 日分时段的厨余垃圾分出量的平均数如下:

( 1 )该小区 5 月 1 日至 30 日的厨余垃圾分出量的平均数约为 (结果取整数)
( 2 )已知该小区 4 月的厨余垃圾分出量的平均数为 ,则该小区 5 月 1 日至 30 日的厨余垃圾分出量的平均数约为 4 月的 倍(结果保留小数点后一位);
( 3 )记该小区 5 月 1 日至 10 日的厨余垃圾分出量的方差为 5 月 11 日至 20 日的厨余垃圾分出量的方差为 , 5 月 21 日至 30 日的厨余垃圾分出量的方差为 .直接写出 的大小关系.
小云在学习过程中遇到一个函数 .下面是小云对其探究的过程,请补充完整:
( 1 )当 时,对于函数 ,即 ,当 时, 随 的增大而 ,且 ;对于函数 ,当 时, 随 的增大而 ,且 ;结合上述分析,进一步探究发现,对于函数 ,当 时, 随 的增大而 .
( 2 )当 时,对于函数 ,当 时, 与 的几组对应值如下表:

综合上表,进一步探究发现,当 时, 随 的增大而增大.在平面直角坐标系 中,画出当 时的函数 的图象.

( 3 )过点 ( )作平行于 轴的直线 ,结合( 1 )( 2 )的分析,解决问题:若直线 与函数 的图象有两个交点,则 的最大值是 .
如图, 为 的直径, 为 延长线上一点, 是 的切线, 为切点, 于点 ,交 于点 .
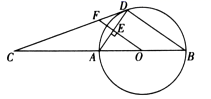
( 1 )求证: ;
( 2 )若 , ,求 的长.
在平面直角坐标系 中,一次函数 的图象由函数 的图象平移得到,且经过点 .
( 1 )求这个一次函数的解析式;
( 2 )当 时,对于 的每一个值,函数 的值大于一次函数 的值,直接写出 的取值范围.
如图,菱形 的对角线 , 相交于点 , 是 的中点,点 在 上, , .

(1 )求证:四边形 是矩形;
( 2 )若 , ,求 和 的长.
已知:如图, 为锐角三角形, .
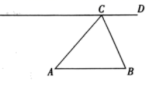
求作:线段 BP ,使得点 P 在直线 CD 上,且 .
作法:①以点 A 为圆心, AC 长为半径画圆,交直线 CD 于 C , P 两点;②连接 BP .线段 BP 就是所求作线段.
( 1 )使用直尺和圆规,依作法补全图形(保留作图痕迹)
( 2 )完成下面的证明.
证明: ,
.
,
∴点 B 在⊙ A 上.
又∵ ( )(填推理依据)
∴
如图,一次函数 图象与反比例函数 的图象交于点 、 ,与 轴交于点 .

( 1 )求一次函数 与反比例函数 的解析式.
( 2 )求点 坐标.
( 3 )平面上的点 与点 、 、 构成平行四边形,请直接写出满足条件的 点坐标 ______ .
某中学开展 " 阳光体育一小时 " 活动,按学校实际情况,决定开设 A :踢毽子; B :篮球; C :跳绳; D :乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如下两个统计图.请结合图中的信息解答下列问题:

(1)本次共调查了 ________ 名学生;
(2)在扇形统计图中, " B " 所在扇形的圆心角是 ________ 度;
(3)将条形统计图补充完整;
(4)若该中学有 1200 名学生,喜欢篮球运动的学生约有 ________ 名.