如图,已知 为 的直径, 、 是 的弦, 是 的切线,切点为 , , 、 的延长线相交于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径.

如图,在 中, ,点 、 分别是 、 的中点.
(1)求证: ;
(2)当四边形 为菱形时,求出该菱形的面积.

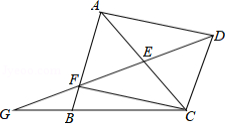
如图,在 中,过点 作 , 是 的中点,连接 并延长,交 于点 ,交 的延长线于点 ,连接 , .
(1)求证:四边形 是平行四边形.
(2)若 , , ,求 的长.
已知线段 直线 于点 ,点 在直线 上,分别以 、 为边作等边三角形 和等边三角形 ,直线 交直线 于点 .
(1)当点 在线段 上时,如图①,求证: ;
(2)当点 在线段 的延长线上时,如图②;当点 在线段 的延长线上时,如图③,请分别写出线段 、 、 之间的数量关系,在图②、图③中选一个进行证明;
(3)在(1)、(2)的条件下,若 , ,则 .

在四边形 中, ,对角线 平分 .
(1)如图1,若 ,且 ,试探究边 、 与对角线 的数量关系并说明理由.
(2)如图2,若将(1)中的条件“ ”去掉,(1)中的结论是否成立?请说明理由.
(3)如图3,若 ,探究边 、 与对角线 的数量关系并说明理由.

已知 的内切圆 与 、 、 分别相切于点 、 、 ,若 ,如图1.
(1)判断 的形状,并证明你的结论;
(2)设 与 相交于点 ,如图2, ,求 的长.

如图,在矩形 中,对角线 的垂直平分线 分别交 、 、 于点 、 、 ,连接 和 .
(1)求证:四边形 为菱形;
(2)若 , ,求菱形 的周长.

如图,在 中, , 于点 , 于点 , 与 交于点 , 于点 ,点 是 的中点,连接 并延长交 于点 .
(1)如图①所示,若 ,求证: ;
(2)如图②所示,若 ,如图③所示,若 (点 与点 重合),猜想线段 、 与 之间又有怎样的数量关系?请直接写出你的猜想,不需证明.

如图, 是正方形 的对角线,线段 在其所在的直线上平移,将平移得到的线段记为 ,连接 ,过点 作 ,垂足为 ,连接 、 .
(1)如图①所示,求证: ;
(2)如图②所示, 在 的延长线上,如图③所示, 在 的反向延长线上,猜想线段 、 之间有怎样的数量关系?请直接写出你的猜想,不需证明.

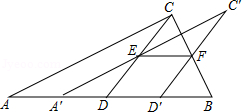
如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
如图,矩形 的对角线 , 相交于点 ,点 , 在 上, .
(1)求证: ;
(2)若 , ,求矩形 的面积.
