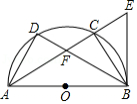
如图, 是半圆 的直径, , 是半圆 上不同于 , 的两点, , 与 相交于点 . 是半圆 所在圆的切线,与 的延长线相交于点 .
(1)求证: ;
(2)若 ,求证: 平分 .
在 中, , 绕点 顺时针旋转到 的位置,点 在斜边 上,连接 ,过点 作 于点 .
(1)如图1,若点 与点 重合,求证: ;
(2)若 ,
①如图2,当点 在线段 的延长线上时,判断线段 与线段 的数量关系,并说明理由;
②当点 在线段 上时,设 ,请用含 的代数式表示线段 .

如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证: ;
(2)连接BF,若 , , 求平行四边形ABCD的面积.

如图,在矩形 中,点 在边 上,且 ,过点 作 ,垂足为点
(1)求证: ;
(2)以 为圆心, 长为半径作圆弧交 于点 ,若 ,求扇形 的面积.(结果保留
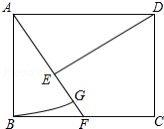
如图,在矩形 中,对角线 的垂直平分线 分别交 、 、 于点 、 、 ,连接 和 .
(1)求证:四边形 为菱形;
(2)若 , ,求菱形 的周长.

如图,在 中, , 于点 , 于点 , 与 交于点 , 于点 ,点 是 的中点,连接 并延长交 于点 .
(1)如图①所示,若 ,求证: ;
(2)如图②所示,若 ,如图③所示,若 (点 与点 重合),猜想线段 、 与 之间又有怎样的数量关系?请直接写出你的猜想,不需证明.

如图, 是正方形 的对角线,线段 在其所在的直线上平移,将平移得到的线段记为 ,连接 ,过点 作 ,垂足为 ,连接 、 .
(1)如图①所示,求证: ;
(2)如图②所示, 在 的延长线上,如图③所示, 在 的反向延长线上,猜想线段 、 之间有怎样的数量关系?请直接写出你的猜想,不需证明.

已知 是等腰三角形,
是等腰三角形, .
.
(1)特殊情形:如图1,当 时,有
时,有
 .(填“
.(填“ ”,“
”,“  ”或“
”或“ ”
” 
(2)发现探究:若将图1中的 绕点
绕点 顺时针旋转
顺时针旋转 到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3, 是等腰直角三角形
是等腰直角三角形 内一点,
内一点, ,且
,且 ,
, ,
, ,求
,求 的度数.
的度数.

已知正方形 ,点
,点 在直线
在直线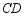 上.
上.
(1)若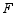 是直线
是直线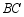 上一点,且
上一点,且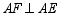 ,求证:
,求证: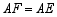 ;(请利用图1所给的图形加以证明)
;(请利用图1所给的图形加以证明)
(2)写出(1)中命题的逆命题,并画出一个图形说明该逆命题是假命题;
(3)若点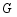 在直线
在直线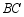 上,且
上,且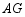 平分
平分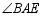 ,探索线段
,探索线段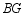 、
、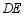 、
、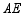 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
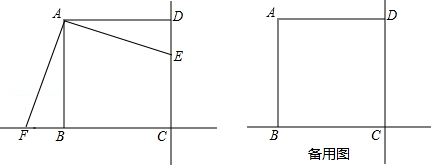
如图,在四边形 ABCD中,∠ B=∠ C=90°, AB> CD, AD= AB+ CD.
(1)利用尺规作∠ ADC的平分线 DE,交 BC于点 E,连接 AE(保留作图痕迹,不写作法);
(2)在(1)的条件下,
①证明: AE⊥ DE;
②若 CD=2, AB=4,点 M, N分别是 AE, AB上的动点,求 BM+ MN的最小值.
