在 中， ， 绕点 顺时针旋转到 的位置，点 在斜边 上，连接 ，过点 作 于点 ．
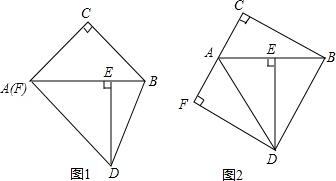
（1）如图1，若点 与点 重合，求证： ；
（2）若 ，
①如图2，当点 在线段 的延长线上时，判断线段 与线段 的数量关系，并说明理由；
②当点 在线段 上时，设 ，请用含 的代数式表示线段 ．
已知：抛物线
经过坐标原点．
（1）求抛物线的解析式和顶点B的坐标；
（2）设点A是抛物线与
轴的另
一个交点，试在
轴上确定一点P，使PA+PB最短，并求出点P的坐标；
（3）过
点A作AC∥BP
交轴于点C，求到直线AP、AC、CP距离相等的点的坐标．
已知点A，B分别是两条平行线
，
上任意两点，C是直线上一点，且
∠ABC=90°，点E在AC的延长线上,BC＝
AB (k≠0).
（1）当＝1
时，在图（1）中，作∠BEF＝∠ABC，EF交直线于点F.，写出线段EF与
EB的数量关系，并加以证明；
（2）若≠1，如图(2)，∠BEF＝∠ABC，其它条件不变，探究线段EF与EB的数量关系，并说明理由．
已知二次函数
的图象经过点
，和
，反比例
函数
（x＞0）的图象经过点（1，2）．
（1）求这两个二次函数的解析式，并在给定的直角坐标系中作出这两个函数的图象；
（2）若反比例函数（
）的图象与二次函数）的图象
在第一象限内交于点
，
落在两个相邻的正整数之间．请你观察图象写出这两个相邻的正整数；
（3）若反比例函数
（
）的图象与二次函数的
图象在第一象限内的交点为
，点的横坐标满足
，试求实数
的取值范围．
一种电讯信号转发装置的发射直径为31km．现要求：在一边长为30km的正方
形城区选择若干个安装点，每个点安装一个这种转发装置
，使这些装置转发的信号能完全
覆盖这个城市．问：
（1）能否找到这样的4个安装点，使得这些点安装了这种转发装置后能
达到预设的要求？在图1中画出安装点的示意图，并用大写字母M、N、P、Q表示安装点；
（2）能否找到这样的3个安装点，使得在这些点安装了这种转发装置后能达到预设的要求？在图2中画出示意图说明，并用大写字母M、N、P表示安装点，用计算、推理和文字来说明你的理由．
粤公网安备 44130202000953号