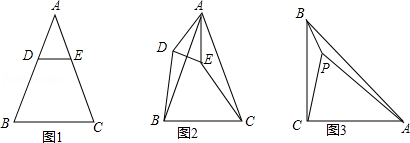
已知 是等腰三角形,
是等腰三角形,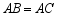 .
.
(1)特殊情形:如图1,当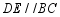 时,有
时,有
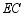 .(填“
.(填“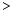 ”,“
”,“ 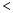 ”或“
”或“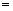 ”
” 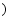
(2)发现探究:若将图1中的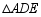 绕点
绕点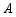 顺时针旋转
顺时针旋转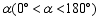 到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,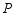 是等腰直角三角形
是等腰直角三角形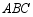 内一点,
内一点,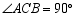 ,且
,且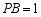 ,
,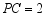 ,
,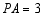 ,求
,求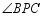 的度数.
的度数.
相关知识点
推荐套卷
已知 是等腰三角形,
是等腰三角形,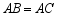 .
.
(1)特殊情形:如图1,当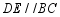 时,有
时,有
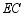 .(填“
.(填“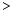 ”,“
”,“ 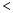 ”或“
”或“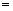 ”
” 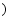
(2)发现探究:若将图1中的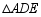 绕点
绕点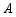 顺时针旋转
顺时针旋转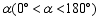 到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,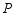 是等腰直角三角形
是等腰直角三角形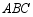 内一点,
内一点,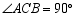 ,且
,且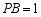 ,
,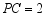 ,
,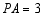 ,求
,求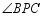 的度数.
的度数.
