如图,沿 方向开山修路.为了加快施工进度,要在小山的另一边同时施工,从 上的一点 取 , , .那么另一边开挖点 离 多远正好使 , , 三点在一直线上 取1.732,结果取整数)?

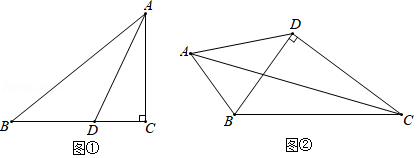
如果三角形的两个内角 与 满足 ,那么我们称这样的三角形为“准互余三角形”.
(1)若 是“准互余三角形”, , ,则 ;
(2)如图①,在 中, , , .若 是 的平分线,不难证明 是“准互余三角形”.试问在边 上是否存在点 (异于点 ,使得 也是“准互余三角形”?若存在,请求出 的长;若不存在,请说明理由.
(3)如图②,在四边形 中, , , , ,且 是“准互余三角形”,求对角线 的长.
如图,在 中, , , .
(1)求 边上的高线长.
(2)点 为线段 的中点,点 在边 上,连结 ,沿 将 折叠得到 .
①如图2,当点 落在 上时,求 的度数.
②如图3,连结 ,当 时,求 的长.

如图,在 中, 的平分线 交 边于点 , 于点 .已知 , .
(1)求证: ;
(2)若 ,求 的面积.

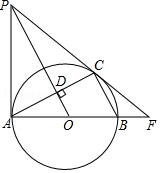
已知:如图,在 中, , 与 相切于点 .求证: .小明同学的证明过程如下框:
证明:连结 , , , 又 , , . |
小明的证法是否正确?若正确,请在框内打“ ”;若错误,请写出你的证明过程.
在菱形 中, ,点 是射线 上一动点,以 为边向右侧作等边 ,点 的位置随着点 的位置变化而变化.

(1)如图1,当点 在菱形 内部或边上时,连接 , 与 的数量关系是 , 与 的位置关系是 ;
(2)当点 在菱形 外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由(选择图2,图3中的一种情况予以证明或说理);
(3)如图4,当点 在线段 的延长线上时,连接 ,若 , ,求四边形 的面积.
如图, 、 分别是 的直径和弦, 于点 .过点 作 的切线与 的延长线交于点 , 、 的延长线交于点 .
(1)求证: 是 的切线;
(2)若 , ,求线段 的长.
如图,在 中,点 、 分别在边 、 的延长线上,且 , 分别与 、 交于点 、 .求证: .
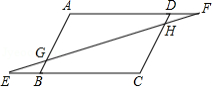
如图,在圆 中,弦 等于弦 ,且相交于点 ,其中 、 为 、 中点.
(1)证明: ;
(2)连接 、 、 ,若 ,证明:四边形 为矩形.

如图, 是 的直径,点 在 上, 垂直于过点 的切线,垂足为 , 垂直 ,垂足为 .延长 交 于点 ,连接 , 与 相交于点 ,连接 .
(1)求证: ;
(2)若 ,求证: 是等腰直角三角形.

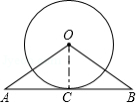
在 中,弦 与直径 相交于点 , .
(Ⅰ)如图①,若 ,求 和 的大小;
(Ⅱ)如图②,若
,过点
作
的切线,与
的延长线相交于点
,求
的大小.
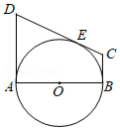
如图所示, 是 的直径, 和 分别切 于 , 两点, 与 有公共点 ,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.