在菱形 中， ，点 是射线 上一动点，以 为边向右侧作等边 ，点 的位置随着点 的位置变化而变化．
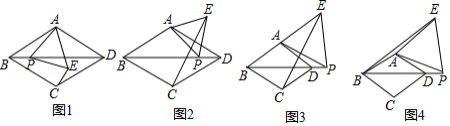
（1）如图1，当点 在菱形 内部或边上时，连接 ， 与 的数量关系是 ， 与 的位置关系是 ；
（2）当点 在菱形 外部时，（1）中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由（选择图2，图3中的一种情况予以证明或说理）；
（3）如图4，当点 在线段 的延长线上时，连接 ，若 ， ，求四边形 的面积．
相关试题
某校数学兴趣小组成员高超对本班上期期末考试数学成绩（成绩取整数，满分为100分）作了统计分析，绘制成如下频数、频率分布表和频数分布直方图．
| 分组 |
49.5～59.5 |
59.5～69.5 |
69.5～79.5 |
79.5～89.5 |
89.5～100.5 |
合计 |
| 频数 |
2 |
a |
20 |
16 |
4 |
n |
| 占调查总人数的 百分比 |
4% |
16% |
m |
32% |
b |
1 |
请你根据图表提供的信息，解答下列问题：
（1）分布表中a= _______ ，b= _______ ；m=，n=。
（2）补全频数分布直方图；
（3）数学老师准备从不低于90分的学生中选1人介绍学习经验，那么取得了97分的高超被选上的百分比是多少？
（4）如图80分以上为优秀，已知该年级共有学生1200人，请你估计一下这次考试优秀人数是多少？
小明家距离学校8千米，今天早晨小明骑车上学途中，自行车突然“爆胎”，恰好路边有便民服务点，几分钟后车修好了，他加快速度骑车到校，我们根据小明的这段经历画了一幅图象，该图描绘了小明行驶路程s与所用时间t之间的函数关系，请根据图象回答下列问题：
（1）小明骑车行驶了多少千米时，自行车“爆胎”修车用了几分钟？
（2）小明共用多长时间到学校的？
（3）小明修车前的速度和修车后的速度分别是多少？
（4）如果自行车未“爆胎”，小明一直按修车前速度行驶，那么他比实际情况早到或晚到多少分钟？
相关知识点
推荐套卷
粤公网安备 44130202000953号