如图,已知一次函数 与反比例函数 的图象交于 , 两点.
(1)求一次函数与反比例函数的解析式;
(2)请根据图象直接写出 时 的取值范围.

如图所示, 的直角顶点 在函数 的图象上,顶点 、 在函数 的图象上, 轴,连接 , ,记 的面积为 , 的面积为 ,设 .
①求 的值以及 关于 的表达式;
②若用 和 分别表示函数 的最大值和最小值,令 ,其中 为实数,求 .

如图,直线 与双曲线 为常数, 在第一象限内交于点 ,且与 轴、 轴分别交于 , 两点.
(1)求直线和双曲线的解析式;
(2)点 在 轴上,且 的面积等于2,求 点的坐标.

如图所示,一次函数 为常数)的图象与反比例函数 的图象都经过点 .
(1)求点 的坐标及一次函数的解析式;
(2)根据图象直接回答:在第一象限内,当 取何值时 .

已知反比例函数 的图象过点 .
(1)求反比例函数的解析式;
(2)若一次函数 的图象与反比例函数的图象只有一个交点,求一次函数的解析式.
已知反比例函数 的图象与一次函数 的图象交于点 和点 .
(1)求这两个函数的表达式;
(2)根据图象直接写出一次函数的值大于反比例函数的值的 的取值范围.
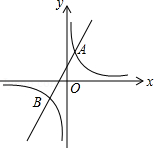
如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于 、 两点,与 轴交于 点,点 的坐标为 ,点 的坐标为 ,且 .
(1)求该反比例函数和一次函数的解析式;
(2)求点 的坐标.

如图,直线 与 轴交于点 ,与 轴交于点 ,将线段 绕点 顺时针旋转 得到线段 ,反比例函数 的图象经过点 .
(1)求直线 和反比例函数 的解析式;
(2)已知点 是反比例函数 图象上的一个动点,求点 到直线 距离最短时的坐标.

在平面直角坐标系中,矩形 的顶点坐标为 , , , , , 交于点 .
(1)如图(1),双曲线 过点 ,直接写出点 的坐标和双曲线的解析式;
(2)如图(2),双曲线 与 , 分别交于点 , ,点 关于 的对称点 在 轴上.求证 ,并求点 的坐标;
(3)如图(3),将矩形 向右平移 个单位长度,使过点 的双曲线 与 交于点 .当 为等腰三角形时,求 的值.

已知反比例函数 的图象经过点 ,点 与点 关于原点 对称, 轴于点 , 轴于点 .
(1)求这个反比例函数的解析式;
(2)求 的面积.

如图,一次函数 与反比例函数 的图象交于 、 两点,与坐标轴分别交于 、 两点.
(1)求一次函数的解析式;
(2)根据图象直接写出 中 的取值范围;
(3)求 的面积.

如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于点 和 .
(1)求一次函数和反比例函数的表达式;
(2)请直接写出 时, 的取值范围;
(3)过点 作 轴, 于点 ,点 是直线 上一点,若 ,求点 的坐标.
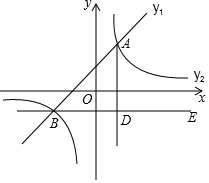
如图,一次函数 的图象与反比例函数 为常数且 的图象交于 , 两点,与 轴交于点 .
(1)求此反比例函数的表达式;
(2)若点 在 轴上,且 ,求点 的坐标.

如图,一次函数 的图象与反比例函数 的图象交于 , , 两点,直线 与 轴交于点 .
(1)求一次函数与反比例函数的解析式;
(2)求 的面积.
