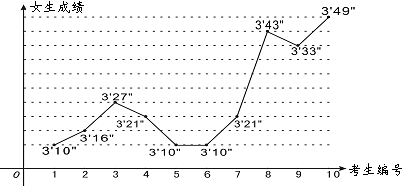
下列图表是某校今年参加中考体育的男生1000米跑、女生800米跑的成绩中分别抽取的10个数据.
考生
编号
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
男生
成绩
|
3′05〞
|
3′11〞
|
3′53〞
|
3′10〞
|
3′55〞
|
3′30〞
|
3′25〞
|
3′19〞
|
3′27〞
|
3′55〞
|
(1)求出这10名女生成绩的中位数、众数和极差;
(2)按规定,男生1000米跑成绩不超过3′35〞就可以得满分.该校学生有490人,男生比女生少70人. 请你根据上面抽样的结果,估算该校考生中有多少名男生该项考试得满分?