(本小题满分12分)一厂家向用户提供的一箱产品共10件,其中有2件次品,
用户先对产品进行抽检以决定是否接收.抽检规则是:一次取一件产品检查(取出的产品不
放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一旦抽查到次品
就立即停止抽检,并且用户拒绝接收这箱产品.
(1)求这箱产品被用户接收的概率;
(2)记抽检的产品件数为 ,求
,求 的分布列和数期望.
的分布列和数期望.
(本小题满分12分)已知函数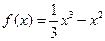 .
.
(1)求f (x)的极值;
(2)已知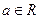 ,设函数
,设函数 的单调递减区间为
的单调递减区间为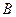 ,且
,且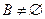 ,
,
函数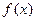 的单调递减区间为
的单调递减区间为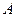 ,若
,若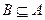 ,求
,求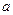 的取值范围.
的取值范围.
(本题满分12分)
已知斜三棱柱 的各棱长均为2, 侧棱
的各棱长均为2, 侧棱 与底面
与底面 所成角为
所成角为 ,且侧面
,且侧面 底面
底面 .
. (1)证明:点
(1)证明:点 在平面
在平面 上的射影
上的射影 为
为 的中点;
的中点;


 (2)求二面角
(2)求二面角 的大小 ;
的大小 ;
(本小题满分12分)已知等差数列 的公差大于0,且
的公差大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前n项的和为
的前n项的和为 ,且
,且 .
.
(1) 求数列 ,
, 的通项公式;
的通项公式;
(2) 记 ,求证:
,求证: .
.
(本题满分12分)在平面直角坐标系中, 的两个顶点
的两个顶点 的坐标分别为
的坐标分别为 ,平面内两点
,平面内两点 同时满足一下条件:①
同时满足一下条件:① ;②
;② ;③
;③
(1)求 的顶点
的顶点 的轨迹方程;
的轨迹方程;
(2)过点 的直线
的直线 与(1)中的轨迹交于
与(1)中的轨迹交于 两点,求
两点,求 的取值范围。
的取值范围。
(本小题满分12分)在一个选拔项目中,每个选手都需要进行4轮考核,每轮设有一个问题,能正确回答者进入下一轮考核,否则被淘汰。已知某选手能正确回答第一、二、三、四轮问题的概率分别为 、
、 、
、 、
、 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。
(Ⅰ)求该选手进入第三轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率;
(Ⅲ)该选手在选拔过程中回答过的问题个数记为 ,求随机变量
,求随机变量 的分布列和期望。
的分布列和期望。
(本小题满分12分)已知数列 、
、 的前n项和分别为
的前n项和分别为 、
、 ,且满足
,且满足 ,
, 。
。
(Ⅰ)求 、
、 的值,并证明数列
的值,并证明数列 是等比数列;
是等比数列;
(Ⅱ)试确定实数 的值,使数列
的值,使数列 是等差数列。
是等差数列。
(本小题满分14分)
已知函数 的图象经过点
的图象经过点 和
和 ,记
,记
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,若
,若 ,求
,求 的最小值;
的最小值;
(Ⅲ)求使不等式 对一切
对一切 均成立的最大实数
均成立的最大实数 。
。