对于函数①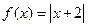 ,②
,②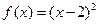 ,③
,③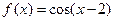 ,判断如
,判断如
下两个命题的真假:
命题甲: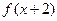 是偶函数;
是偶函数;
命题乙: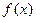 在
在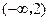 上是减函数,在
上是减函数,在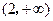 上是增函数;
上是增函数;
能使命题甲、乙均为真的所有函数的序号是
如右图,在正方形内有一扇形(见阴影部分),扇形对应的圆心是正方形的一顶点,半径为正方形的边长。在这个图形上随机撒一粒黄豆,它落在扇形外正方形内的概率为 。(用分数表示)
在平面直角坐标系中,定义 为两点
为两点 之间的“折线距离”,在这个定义下,给
之间的“折线距离”,在这个定义下,给 出下列命题:
出下列命题:
①到原点的“折线距离”等于1 的点的集合是一个正方形;
②到原点的“折线距离”等于1 的点的集合是一个圆;
③到 两点的“折线距离”之
两点的“折线距离”之 和为4的点的集合是面积为6的六边形;
和为4的点的集合是面积为6的六边形;
④到 两点的“折线距离”差的绝对值为1的点的集合是两条平行线;
两点的“折线距离”差的绝对值为1的点的集合是两条平行线;
其中正确的命题是  。(写出所有正确命题的序号)
。(写出所有正确命题的序号)
用“二分法”求方程 在区间
在区间 内的实根,取区间中点为
内的实根,取区间中点为 ,那么下一个有根的区间是 。
,那么下一个有根的区间是 。
若数列 满足:对任意的
满足:对任意的 ,只有有限个正整数
,只有有限个正整数 使得
使得 成立,记
成立,记
这样的 的个数为
的个数为 ,则得到一个新数列
,则得到一个新数列 .例如,若数列
.例如,若数列 是
是 ,
,
则数列 是
是 .已知对任意的
.已知对任意的 ,
, ,则
,则 ,
,
 .
.
在平面直角坐标系中,双曲线 的中心在原点,它的一个焦点坐标为
的中心在原点,它的一个焦点坐标为 ,
, 、
、 分别是两条渐近线的方向向量。任取双曲线
分别是两条渐近线的方向向量。任取双曲线 上的点
上的点 ,若
,若 (
( 、
、 ),则
),则 、
、 满足的一个等式是 .
满足的一个等式是 .
已知变量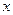 ,
,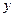 满足约束条件
满足约束条件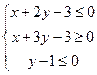 。若目标函数
。若目标函数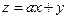 (其中
(其中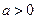 )
)
仅在点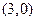 处取得最大值,则
处取得最大值,则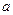 的取值范围为 。
的取值范围为 。
植树节某班20名同学在一段直线公路一侧植树,每人植一棵,相邻两棵树相距10米.开始时需将树苗集中放置在某一树坑旁边,使每位同学从各自树坑出发前来领取树苗往返所走的路程总和最小,这个最小值为 (米).