2012届新人教版高三上学期单元测试(5)数学试卷
“公差为0的等差数列是等比数列”;“公比为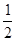 的等比数列一定是递减数列”;“a,b,c
的等比数列一定是递减数列”;“a,b,c
三数成等比数列的充要条件是b2=ac”;“a,b,c三数成等差数列的充要条件是2b=a+c”,以上
四个命题中,正确的有 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知数列{an}中,an= (n∈N),则数列{an}的最大项是( )
(n∈N),则数列{an}的最大项是( )
| A.第12项 | B.第13项 |
| C.第12项或13项 | D.不存在 |
在等差数列中,前n项的和为Sn,若Sm=2n,Sn=2m,(m、n∈N且m≠n),则公差d
的值为( )
A.- |
B.- |
C.- |
D.- |
设 是任意等比数列,它的前
是任意等比数列,它的前 项和,前
项和,前 项和与前
项和与前 项和分别为
项和分别为 ,
,
则下列等式中恒成立的是 ( )
A. |
B. |
C. |
D. |
已知 是首项为1的等比数列,
是首项为1的等比数列, 是
是 的前n项和,且
的前n项和,且 ,则数列
,则数列
的前5项和为 ( )
A. 或5 或5 |
B. 或5 或5 |
C. |
D. |
a、b∈R,且|a|<1,|b|<1,则无穷数列:1,(1+b)a,(1+b+b2)a2,…,(1+b+b2+…
+bn-1)an-1…的和为 ( )
A. |
B. |
C. |
D. |
若钝角三角形三内角的度数成等差数列,且最大边长与最小边长的比值为m,则
m的范围是( )
| A.(1,2) | B.(2, +∞) +∞) |
C.[3,+∞ |
D.(3,+∞) |
如图,在半径为r 的圆内作内接正六边形,再 作正六边形的内切圆,又在此内切
作正六边形的内切圆,又在此内切
圆内作内接正六边形,如此无限继续下去,设 为前n个圆的面积之和,则
为前n个圆的面积之和,则
 =( )
=( )
A.2 |
B.  |
C.4 |
D.6 |
若数列{an}前8项的值各异,且an+8=an对任意n∈N*都成立,则下列数列中可取
遍{an}前8项值的数列为 ( )
| A.{a2k+1} | B.{a3k+1} | C.{a4k+1} | D.{a6k+1} |
根据市场调查结果,预测某种家用商品从年初开始的n个月内累积的需求量Sn
(万件)近似地满足Sn= (21n-n2-5)(n=1,2,……,12),按此预测,在本年度内,
(21n-n2-5)(n=1,2,……,12),按此预测,在本年度内,
需求量超过1.5万件的月份是 ( )
| A.5月、6月 | B.6月、7月 | C.7月、8月 | D.8月、9月 |
作边长为a的正三角形的内切圆,在这个圆内作新的内接正三角形,在新的正三
角形内再作内切圆,如此继续下去,所有这些圆的周长之和及面积之和分别为________。
在直角坐标系中,O是坐标原点,P1(x1,y1)、P2(x2,y2)是第一象限的两个
点,若1,x1,x2,4依次成等差数 列,而1,y1,y2,8依次成等比数列,则△OP1P2的面
列,而1,y1,y2,8依次成等比数列,则△OP1P2的面
积是________。
若数列 满足:对任意的
满足:对任意的 ,只有有限个正整数
,只有有限个正整数 使得
使得 成立,记
成立,记
这样的 的个数为
的个数为 ,则得到一个新数列
,则得到一个新数列 .例如,若数列
.例如,若数列 是
是 ,
,
则数列 是
是 .已知对任意的
.已知对任意的 ,
, ,则
,则 ,
,
 .
.
在数列 中,
中, =0,且对任意k
=0,且对任意k ,
, 成等差数列,
成等差数列,
其公差为2k。
(Ⅰ)证明 成等比数列;
成等比数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
 证明以下命题:
证明以下命题:
(Ⅰ)对任一正整a,都存在整数b,c(b<c),使得 成等差数列。
成等差数列。
(Ⅱ)存在无穷多个互不相似的三角形△ ,其边长
,其边长 为正整数且
为正整数且 成等差数列。
成等差数列。
设

 ,若将
,若将
适当排序后可构成公差为1的等差数列 的前三项.
的前三项.
(Ⅰ)求
 的值及
的值及 的通项公式;
的通项公式;
(Ⅱ )记函数
)记函数 的图象在
的图象在 轴上截得的线段长为
轴上截得的线段长为 ,设
,设 ,求
,求
设各项均为正数的数列 的前n项和为
的前n项和为 ,已知
,已知 ,数
,数
列 是公差为
是公差为 的等差数列。
的等差数列。
(1)求数列 的通项公式(用
的通项公式(用 表示);
表示);
(2)设 为实数,对满足
为实数,对满足 的任意正整数
的任意正整数 ,不等式
,不等式 都成立。求证:
都成立。求证: 的最大值为
的最大值为 。
。
 }中,各项都是正数,且
}中,各项都是正数,且 ,
, 成等差数列,则
成等差数列,则




 的图象在下列图中,并且对任意
的图象在下列图中,并且对任意 ,由关系式
,由关系式 得到的数列
得到的数列 满足
满足 ,则该函数的图象是( )
,则该函数的图象是( )
 的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q
的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q 为等差数列,且
为等差数列,且 ,
, 。
。 满足
满足 ,
, ,求
,求 下面的数表序列:
下面的数表序列:
 )有n行,第1行的n个数是1,3,5,
)有n行,第1行的n个数是1,3,5, ,每行中的每个数都等
,每行中的每个数都等 于它肩上的两数之和。
于它肩上的两数之和。 ,记此数列为
,记此数列为 求和:
求和:

 粤公网安备 44130202000953号
粤公网安备 44130202000953号