高中数学解答题

已知集合A=， B=，求：
（1） 
（2）

(本小题满分12分)已知二次函数对任意实数x都满足
，且．令.
（1）求的表达式；
（2）设，证明：对任意，恒有．

(本小题满分12分)已知数列的首项
（1）求的通项公式；
（2）证明：对任意的．

(本小题满分12分)
设函数，已知是奇函数．
（1）求b、c的值；
（2）求的单调区间与极值．

(本题12分)已知，解关于的不等式.

（本题12分）已知等差数列满足：的前项和；
(1)求；
(2)令，求数列的前项和.

已知向量a＝(,1)，b＝(－2，k)
（1）k为何值时，a∥b？
（2）k为何值时，a⊥b？
（3）k为何值时，a、b夹角为120°？

请你设计一个包装盒，如图所示，ABCD是边长为60cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得ABCD四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒，E、F在AB上是被切去的等腰直角三角形斜边的两个端点，设AE＝FB＝xcm．
（1）若广告商要求包装盒侧面积S（cm）最大，试问x应取何值？
（2）若广告商要求包装盒容积V（cm）最大，试问x应取何值？并求出此时包装盒的高与底面边长的比值．

已知椭圆C：＋y²＝1，过点(m,0)作圆x²＋y²＝1的切线l交椭圆G于A、B两点．
（1）求椭圆C的焦点坐标和离心率；
（2）将|AB|表示为m的函数，并求|AB|的最大值

已知在一个二阶矩阵M的变换作用下, 点变成了点，点变成了点，求矩阵M.

设,.
（1）当=2011时,记，
求；
（2）若展开式中的系数是20，则当、变化时，试求系数的最小值．

在四棱锥中，底面是边长为1的菱形，, 底面, ,为的中点
（1）求异面直线AB与MD所成角的大小；
（2）求平面与平面所成的二面角的余弦值.

某电器商经过多年的经验发现本店每个月售出的电冰箱的台数是一个随机变量，它的分布列为： ；设每售出一台电冰箱，电器商获利300元.如销售不出，则每台每月需花保管费100元. 问电器商每月初购进多少台电冰箱才能使月平均收益最大？

如图，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘渔船遇险等待营救．甲船立即前往救援，同时把消息告知在甲船的南偏西30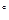，相距10海里C处的乙船，试问乙船应朝北偏东多少度的方向沿直线前往B处救援（已知sin41°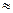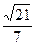，角度精确到1）？

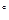如图所示，扇形AOB，圆心角AOB等于60°，半径为2，在弧AB上有一动点P，过P引平行于OB的直线和OA交于点C，设∠AOP＝θ，求△POC面积的最大值及此时θ的值．