高中数学解答题

已知是定义在R上的函数，对于任意的,,且当 时，．
（1）求的解析式；
（2）画出函数的图象，并指出的单调区间及在每个区间上的增减性；
（3）若函数f（x）在区间[－1，a－2]上单调递增，试确定a的取值范围.

设函数y=是定义在（0，+∞）上的增函数，并满足
1、求f(1)的值；
2、若存在实数m，使，求m的值
3、如果<２求x的范围

如图，三角形ABC中，AC=BC=，ABED是边长为1的正方形，平面ABED⊥底面ABC，若G、F分别是EC、BD的中点．
（１）求证：GF//底面ABC；
（２）求证：AC⊥平面EBC；
（３）求几何体ADEBC的体积V．

在正三角形ABC中，E、F、P分别是AB、AC、BC边上的点，满足AE:EB＝CF:FA＝CP:PB＝1:2（如图1）。将△AEF沿EF折起到的位置，使二面角A₁－EF－B成直二面角，连结A₁B、A₁P（如图2）
（Ⅰ）求证：A₁E⊥平面BEP；
（Ⅱ）求二面角A₁－BP－E的大小。

（本小题满分14分）
已知圆C：，是否存在斜率为1的直线l，使l被圆C截得的弦AB为直径的圆过原点，若存在,求出直线l的方程;若不存在说明理由。

（本小题満分12分）已知中心在原点的双曲线C的右焦点为（2,0），右顶点为。
（1）求双曲线C的方程；
（2）若直线l：与双曲线C恒有两个不同的交点A和B，且（其中O为原点），求k的取值范围。

已知直线经过直线与直线的交点，且垂直于直线.
（Ⅰ）求直线的方程；
（Ⅱ）求直线与两坐标轴围成的三角形的面积.

已知为等差数列，且，
（1）求的通项公式；
（2）若等差数列满足，，求的前n项和．

制定投资计划时，不仅要考虑可能获得的赢利，而且要考虑可能出现的亏损。某投资人打算投资甲、乙两个项目，根据预测，甲、乙项目可能的最大赢利率分别为100％和50％，可能的最大亏损率分别为30％和10％，投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元，问投资人对甲、乙两个项目各投资多少万元，才能使可能的赢利最大？                                                      

（本小题满分12分）
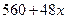某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层、每层2000平方米的楼房．经测算，如果将楼房建为层，则每平方米的平均建筑费用为（单位：元）．为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？
（注：平均综合费用平均建筑费用平均购地费用，平均购地费用）

(本小题满分12分)
已知数列是等差数列，；数列的前n项和是，且．
(Ⅰ) 求数列的通项公式；
(Ⅱ) 求证：数列是等比数列；
(Ⅲ) 记，求的前n项和．

计算：
（1)
（2）

已知指数函数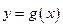满足：g(3)=8，定义域为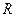的函数是奇函数.
（1）确定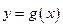的解析式；
（2）求m，n的值；
（3）若对任意的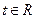，不等式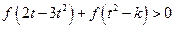恒成立，求实数的取值范围

运货卡车以每小时x千米的速度匀速行驶130千米(50≤x≤100)(单位：千米/小时)．假设汽油的价格是每升2元，而汽车每小时耗油(2＋)升，司机的工资是每小时14元
(Ⅰ)求这次行车总费用y关于x的表达式
(Ⅱ)当x为何值时，这次行车的总费用最低，并求出最低费用的值

已知直线：，，，
(Ⅰ)求与交点的坐标；
(Ⅱ)求过点，且与垂直的直线方程.