高中数学解答题

在△ABC中，BC＝，AC＝3，sin C＝2sin  A.
(1)求AB的值；
(2)求sin的值．

（1）化简
（2）计算的值

已知定义域为的函数是奇函数。
（Ⅰ）求的值；
（Ⅱ）若对任意的，不等式恒成立，求的取值范围；

对于定义域为D的函数，若同时满足下列条件：①在D内单调递增或单调递减；②存在区间[]，使在[]上的值域为[]；那么把()叫闭函数。
（1）求闭函数符合条件②的区间[]；
（2）判断函数是否为闭函数？并说明理由；
（3）若函数是闭函数，求实数的取值范围

已知椭圆的离心率为，过右顶点的直线与椭圆相交于、两点，且.
（1）求椭圆和直线的方程；
（2）记曲线在直线下方的部分与线段AB所围成的平面区域（含边界）为．若曲线与有公共点，试求实数的最小值．

已知椭圆G:.过点（m,0），作圆的切线,交椭圆G于A，B两点.
（I）求椭圆G的焦点坐标和离心率；  （II）将表示为m的函数，并求的最大值.

选修4-5：不等式选讲
已知函数不等式的解集为
（1）求实数a的值；
（2）若对一切实数x恒成立，求实数c的取值范围。

（本小题满分12分）。
如图，过抛物线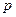（＞0）的顶点作两条互相垂直的弦OA、OB。

⑴设OA的斜率为k，试用k表示点A、B的坐标；
⑵求弦AB中点M的轨迹方程。

某单位在抗雪救灾中，需要在A，B两地之间架设高压电线，测量人员在相距6 000 m的C、D两地(A，B，C，D在同一平面上)测得∠ACD＝45°，∠ADC＝75°，∠BCD＝30°，∠BDC＝15°(如图)．假如考虑到电线的自然下垂和施工损耗等原因，实际所需电线长度大约是A、B两地之间距离的1.2倍，问施工单位至少应该准备多长的电线(精确到0.1 m)？(参考数据：≈1.4，≈1.7，≈2.6)

一个多面体的直观图和三视图如下:

(其中分别是中点)
(1)求证:平面;
(2)求多面体的体积.

设椭圆的中心在原点，焦点在x轴上，离心率e＝.已知点P到这个椭圆上的点的最远距离为，求这个椭圆的方程．

求过两直线与的交点且与第一条直线垂直的直线方程

求圆心在直线，并且经过原点和点的圆的方程

（本小题满分13分）某园林公司计划在一块为圆心,（为常数，单位为米）为半径的半圆形（如图）地上种植花草树木，其中弓形区域用于观赏样板地，区域用于种植花木出售，其余区域用于种植草皮出售．已知观赏样板地的成本是每平方米2元，花木的利润是每平方米8元，草皮的利润是每平方米3元．

（1）设, 用表示弓形的面积；
（2）园林公司应该怎样规划这块土地,才能使总利润最大? 并求相对应的

（本小题满分13分）已知曲线，从上的点作轴的垂线，交于点，再从点作轴的垂线，交于点，设．
（1）求数列的通项公式；
（2）记，数列的前项和为，求证：；
（3）若已知，记数列的前项和为，数列的前项和为，试比较与的大小．