高中数学解答题

(本题12分)设函数
⑴求的表达式；
⑵求的单调区间、极大值、极小值。

.(本题12分)已知.
⑴化简并求函数的最小正周期
⑵求函数的最大值，并求使取得最大值的的集合

(本题12分)如图，已知AD为⊙O的直径，直线BA与⊙O相切于点A，直线OB与弦AC垂直并相交于点G.
求证：BA·DC＝GC·AD.

．某市环保研究所对市中心每天环境污染情况进行调查研究后，发现一天中环境综合污染指数与时间x(小时)的关系为，其中是与气象有关的参数，且，若用每天的最大值为当天的综合污染指数，并记作.
(1)令，求t的取值范围；(2)求函数；
(3)市政府规定，每天的综合污染指数不得超过2，试问目前市中心的综合污染是否超标？请说明理由。

已知函数，
（1）求函数的单调区间；
（2）若 恒成立，试确定实数的取值范围；
（3）证明：（且）

（本小题满分12分）已知函数的定义域为集合A, 的值域为集合B.
(1)若,求；
(2) 若,求实数的取值范围。

（本小题满分12分）已知二次函数满足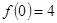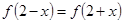：，，且该函数的最小值为2.
⑴ 求此二次函数的解析式;
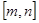⑵ 若函数的定义域为= .(其中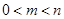). 问是否存在这样的两个实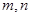数,使得函数的值域也为?若存在,求出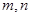的值;若不存在,请说明理由.

（本小题满分12分）已知函数
（1）讨论并证明函数在区间的单调性；
（2）若对任意的恒成立，求实数的取值范围。

（本小题满分13分）有一批单放机原价为每台80元，两个商场均有销售，为了吸引顾客，两商场纷纷推出优惠政策。甲商场的优惠办法是：买一台减4元，买两台每台减8元，买三台每台减12元，......,依此类推，直到减到半价为止；乙商场的优惠办法是：一律7折。某单位欲为每位员工买一台单放机，问选择哪个商场购买比较划算？

（本小题满分12分） 已知的周长为，且．
　　（1）求边长的值；
　　（2）若，求的值．

已知数列的前n项和为，且．
（Ⅰ）求数列通项公式；
（Ⅱ）若，，求数列的前项和．

(12分) 设，．
（1）求在上的值域；
（2）若对于任意，总存在，使得成立，求的取值范围．

(14分)设是椭圆的两点，，，且，椭圆离心率，短轴长为2，O为坐标原点。
(1) 求椭圆方程；
(2) 若存在斜率为的直线AB过椭圆的焦点（为半焦距），求的值；
(3) 试问的面积是否为定值？若是，求出该定值；若不是，说明理由。

已知函数
（Ⅰ）求的值；
（Ⅱ）求的最大值和最小值．

已知O（0，0）、A（，0）为平面内两定点，动点P满足|PO|+|PA|=2．
（I）求动点P的轨迹方程；
（II）设直线与（I）中点P的轨迹交于B、C两点．求△ABC的最大面积及此时直线l的方程。