已知动点M到点A(2,0)的距离是它到点B(8,0)的距离的一半,
求:(Ⅰ)动点M的轨迹方程;
(Ⅱ)若N为线段AM的中点,试求点N的轨迹.
如图,四棱锥 的底面是直角梯形,
的底面是直角梯形, ,
, ,
, 和
和 是两个边长为
是两个边长为 的正三角形,
的正三角形, ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
已知抛物线 的方程 为
的方程 为 ,直线
,直线 与抛物线
与抛物线 相交
相交
于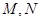 两点,点
两点,点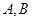 在抛物线
在抛物线 上.(Ⅰ)若
上.(Ⅰ)若 求证:直线
求证:直线
的斜率为定值;
(Ⅱ)若直线 的斜率为
的斜率为 且点
且点 到 直线
到 直线 的距离的和为
的距离的和为 ,试判断
,试判断 的形状,并证明你的结论.
的形状,并证明你的结论.
已知函数 在[1,+∞)上为增函数,且
在[1,+∞)上为增函数,且 ,
, ,
, ∈R.
∈R.
(1)求θ的值;
(2)若 在[1,+∞)上为单调函数,求m的取值范围;
在[1,+∞)上为单调函数,求m的取值范围;
(3)设 ,若在[1,e]上至少存在一个
,若在[1,e]上至少存在一个 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
已知 ,
, ,若动点
,若动点 满足
满足 ,
, 点的轨迹为曲线
点的轨迹为曲线 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)试确定 的取值范围,使得对于直线
的取值范围,使得对于直线 :
: ,曲线
,曲线 上总有不同的两点关于直线
上总有不同的两点关于直线 对称.
对称.
设椭圆 的左,右两个焦点分别为
的左,右两个焦点分别为 ,短轴的上端点为
,短轴的上端点为 ,短轴上的两个三等分点为
,短轴上的两个三等分点为 ,且
,且 为正方形。
为正方形。
(1)求椭圆的离心率;
(2)若过点 作此正方形的外接圆的切线在
作此正方形的外接圆的切线在 轴上的一个截距为
轴上的一个截距为 ,求此椭圆方程。
,求此椭圆方程。
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点, =2
=2 =2.
=2.
(1)求证: ;
;
(2)求证: ∥平面
∥平面 ;
;
(3)求三棱锥 的体积
的体积 .
.
已知A、B两城相距100km,在两地之间距A城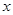 km处D地建一核电站给A、B两城供电,为保证城市安全.核电站距市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数
km处D地建一核电站给A、B两城供电,为保证城市安全.核电站距市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数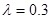 .若A城供电量为20亿度/月,B城为10亿度/月.
.若A城供电量为20亿度/月,B城为10亿度/月.
(1)把月供电总费用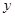 表示成
表示成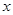 的函数,并求定义域;
的函数,并求定义域;
(2)核电站建在距A城多远,才能使供电费用最小.