[浙江]2012届浙江省台州市高三第二次月考文科数学试卷
若 在椭圆
在椭圆 外 ,则过
外 ,则过 作椭圆的两条切线的切点为
作椭圆的两条切线的切点为 则切点弦
则切点弦 所在直线方程是
所在直线方程是 .那么对于双曲线则有如下命题: 若
.那么对于双曲线则有如下命题: 若 在双曲线
在双曲线
 外 ,则过
外 ,则过 作双曲线的两条切线的切点为
作双曲线的两条切线的切点为 则切点弦
则切点弦 的所在直线方程是
的所在直线方程是
对于给定数列 ,如果存在实常数
,如果存在实常数 ,使得
,使得 对于任意
对于任意 都成立,我们称数列
都成立,我们称数列 是 “
是 “ 类数列”.
类数列”.
(Ⅰ)已知数列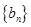 是 “
是 “ 类数列”且
类数列”且 ,求它对应的实常数
,求它对应的实常数 的值;
的值;
(Ⅱ)若数列 满足
满足 ,
, ,求数列
,求数列 的通项公式.并判断
的通项公式.并判断 是否为“
是否为“ 类数列”,说明理由.
类数列”,说明理由.
若 在椭圆
在椭圆 外 ,则过
外 ,则过 作椭圆的两条切线的切点为
作椭圆的两条切线的切点为 则切点弦
则切点弦 所在直线方程是
所在直线方程是 .那么对于双曲线则有如下命题: 若
.那么对于双曲线则有如下命题: 若 在双曲线
在双曲线
 外 ,则过
外 ,则过 作双曲线的两条切线的切点为
作双曲线的两条切线的切点为 则切点弦
则切点弦 的所在直线方程是
的所在直线方程是
对于给定数列 ,如果存在实常数
,如果存在实常数 ,使得
,使得 对于任意
对于任意 都成立,我们称数列
都成立,我们称数列 是 “
是 “ 类数列”.
类数列”.
(Ⅰ)已知数列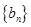 是 “
是 “ 类数列”且
类数列”且 ,求它对应的实常数
,求它对应的实常数 的值;
的值;
(Ⅱ)若数列 满足
满足 ,
, ,求数列
,求数列 的通项公式.并判断
的通项公式.并判断 是否为“
是否为“ 类数列”,说明理由.
类数列”,说明理由.