如图所示,正方形 和矩形
和矩形 所在平面相互垂直,
所在平面相互垂直, 是
是 的中点.
的中点.
(I)求证: ;
;
(Ⅱ)若直线 与平面
与平面 成45o角,求异面直线
成45o角,求异面直线 与
与 所成角的余弦值.
所成角的余弦值.
已知点 及圆
及圆 :
: .
.
(Ⅰ)若直线 过点
过点 且与圆心
且与圆心 的距离为1,求直线
的距离为1,求直线 的方程;
的方程;
(Ⅱ)设过点P的直线 与圆
与圆 交于
交于 、
、 两点,当
两点,当 时,求以线段
时,求以线段 为直径的圆
为直径的圆 的方程;
的方程;
(Ⅲ)设直线 与圆
与圆 交于
交于 ,
, 两点,是否存在实数
两点,是否存在实数 ,使得过点
,使得过点 的直线
的直线 垂直平分弦
垂直平分弦 ?若存在,求出实数
?若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图,在四棱锥A-ABCD中,底面ABCD是正方形,其他四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC上一点.
(1)当E为侧棱SC的中点时,求证:SA∥平面BDE;
(2)求证:平面BDE⊥平面SAC;
(3)当二面角E-BD-C的大小为45°时,试判断点E在SC上的位置,并说明理由.
选修4—4:坐标系与参数方程
以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线 经过点P(1,1),倾斜角
经过点P(1,1),倾斜角 .
.
(1)写出直线 的参数方程;
的参数方程;
(2)设 与圆
与圆 相交于两点A、B,求点P到A、B两点的距离之积.
相交于两点A、B,求点P到A、B两点的距离之积.
设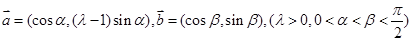 是平面上的两个向量,若向量
是平面上的两个向量,若向量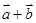 与
与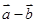 互相垂直.
互相垂直.
(Ⅰ)求实数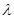 的值;
的值;
(Ⅱ)若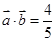 ,且
,且 ,求
,求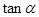 的值.
的值.
在 中,
中, 分别为角
分别为角
 所对的边,且
所对的边,且 ,
,
(Ⅰ)求角 ;
;
(Ⅱ)若 ,
,
 ,
, 的周长为
的周长为 ,求函数
,求函数 的取值范围.
的取值范围.
二次函数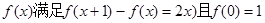
(1)求f(x)的解析式;
(2)在区间[-1,1]上,y= f(x)的图像恒在y=2x+m的图像上方,试确定实数m的取值范围。
已知二次函数 满足:①当
满足:①当 时有极值,②图象与y轴交点的纵坐标为
时有极值,②图象与y轴交点的纵坐标为 ,且在该点处的切线与直线
,且在该点处的切线与直线 垂直
垂直
(I)求f(1)的值
(II)求函数 的值域
的值域
(III)若曲线 上任意一点处的切线的斜率恒大于
上任意一点处的切线的斜率恒大于 ,求
,求 的取值范围
的取值范围